2次不等式のように解く不等式

「次の不等式を実数の範囲で解け。

(1)$\large -2\sin^2\theta-5\sin\theta+3>0\quad(0\leqq\theta<2\pi)$

(2)$\large 2^{2x}-2^{x+1}-8\leqq0$

(3)$\large x+2\sqrt{x}-15>0$」

これらの不等式はどのように解けばよいのでしょうか？

　三角関数や指数関数にはとりうる値の範囲があります。その範囲に注意しながら解を求める必要があります。
また、2次不等式の解き方にはグラフから解く方法と因数に着目して解く方法があります。この2通りの解き方でそれぞれ解いてみます。

関連：2次不等式を解く(2)

(1)$-2\sin^2\theta-5\sin\theta+3>0$

ただし、$0\leqq\theta<2\pi$

　まずは$\sin\theta=t$とおいて、因数分解します。

$$\begin{align*}-2t^2-5t+3&>0\\[0.5em]2t^2+5t-3&<0\\[0.5em](t+3)(2t-1)&<0\end{align*}$$

1. グラフから解く方法

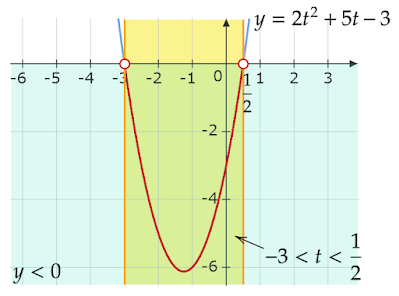
　$2t^2+5t-3<0$より$y=2t^2+5t-3$のグラフを描くと上図のようになります。
不等式は$y<0$の部分を表すのでその部分の$t$、すなわち$\sin\theta$の範囲は

$$-3<\sin\theta<\frac{1}{2}$$

となります。ここで、$-1\leqq\sin\theta\leqq1$という三角関数のとりうる値の範囲があるので、共通範囲は

$$-1\leqq\sin\theta<\frac{1}{2}$$

となります。
このことから$\theta$は$0\leqq\theta<2\pi$より

$$0\leqq\theta<\frac{\pi}{6},\frac{5}{6}\pi<\theta<2\pi$$

となります。

関連：三角関数を含む不等式を解く

2. 因数に着目して解く方法

　$(t+3)(2t-1)<0$、すなわち$(\sin\theta+3)(2\sin\theta-1)<0$より$(\sin\theta+3)(2\sin\theta-1)$は負の数であることがわかります。
掛けて負になるのは$正×負=負,負×正=負$より

$$\begin{gather*}\left\{\begin{aligned}\sin\theta+3&>0\\[1em]2\sin\theta-1&<0\end{aligned}\right.\tag{a}\\ \text{or}\\ \left\{\begin{aligned}\sin\theta+3&<0\\[1em]2\sin\theta-1&>0\end{aligned}\right.\tag{b}\end{gather*}$$

という条件があることがわかります。

ここで、$-1\leqq\sin\theta\leqq1$より$\sin\theta+3$は常に正となることがわかるので、$\text{(b)}$の$\sin\theta+3<0$は成り立たず不適となり$\text{(a)}$に絞り込まれます。
$\text{(a)}$の

$$\begin{align*}2\sin\theta-1&<0\\[0.5em]2\sin\theta&<1\\[0.5em]\sin\theta&<\frac{1}{2}\end{align*}$$

と$-1\leqq\sin\theta\leqq1$より

$$-1\leqq\sin\theta<\frac{1}{2}$$

を解くと$\theta$は$0\leqq\theta<2\pi$より

$$0\leqq\theta<\frac{\pi}{6},\frac{5}{6}\pi<\theta<2\pi$$

となります。
常に正、常に負となるものは、変数に何を代入しても成り立つということなので、範囲を求められません。

(2)$2^{2x}-2^{x+1}-8\leqq0$

　指数の計算法則より

$$\begin{align*}2^{2x}&=\left(2^x\right)^2\\[1em]2^{x+1}&=2\cdot2^x\end{align*}$$

となるので、

$$\left(2^x\right)^2-2\cdot2^x-8\leqq0$$

と書けます。また、$2^x=t$とおいて因数分解すると

$$\begin{align*}t^2-2t-8&\leqq0\\[0.5em](t+2)(t-4)&\leqq0\end{align*}$$

となります。

関連：指数の計算法則

1.の方法

　$y=t^2-2t-8$のグラフは上図のようになり、不等式は$y\leqq0$の部分を表します。
その部分の$t$、すなわち$2^x$の範囲は

$$-2\leqq2^x\leqq4$$

となります。ここで、$2^x>0$という指数関数のとりうる値の範囲があるので、共通範囲は

$$0<2^x\leqq4$$

となります。

底が$1$より大きい指数関数は指数が大きくなるに従って大きくなるので$x$の範囲は

$$\begin{align*}(0<)2^x&\leqq2^2\\[0.5em]x&\leqq2\end{align*}$$

となります。

2.の方法

　$(t+2)(t-4)\leqq0$、すなわち$(2^x+2)(2^x-4)\leqq0$より$(2^x+2)(2^x-4)$は$0$か負の数であることがわかります。

掛けて負になる、または$0$になる条件は

$$\begin{gather*}\left\{\begin{aligned}2^x+2&>0\\[1em]2^x-4&<0\end{aligned}\right.\tag{c}\\ \text{or}\\ \left\{\begin{aligned}2^x+2&<0\\[1em]2^x-4&>0\end{aligned}\right.\tag{d}\\ \text{or}\\ 2^x+2=0\tag{e}\\ \text{or}\\ 2^x-4=0\tag{f}\end{gather*}$$

となります。

ここで、$2^x>0$より$2^x+2$は常に正となることがわかるので、$\text{(d)}$の$2^x+2<0$、$\text{(e)}$の$2^x+2=0$は成り立たず不適であるため、$\text{(c)}$と$\text{(f)}$に絞り込まれます。

$\text{(c)}$のとき

$$\begin{align*}2^x-4&<0\\[0.5em](0<)2^x&<4\\[0.5em]2^x&<2^2\\[0.5em]x&<2\end{align*}$$

$\text{(f)}$のとき

$$\begin{align*}2^x&=4\\[0.5em]2^x&=2^2\\[0.5em]x&=2\end{align*}$$

解は$\text{(c)}$または$\text{(f)}$、すなわち$x<2$または$x=2$なので組み合わせて$x\leqq2$となります。

(3)$x+2\sqrt{x}-15>0$

　$x=\left(\sqrt{x}\right)^2$なので、

$$\left(\sqrt{x}\right)^2+2\sqrt{x}-15>0$$

$\sqrt{x}=t$とおいて因数分解すると

$$\begin{align*}t^2+2t-15&>0\\[0.5em](t+5)(t-3)&>0\end{align*}$$

となります。

1.の方法

　$y=t^2+2t-15$のグラフは上図のようになり、不等式は$y>0$の部分を表します。
その部分の$t$、すなわち$\sqrt{x}$の範囲は

$$\sqrt{x}<-5,3<\sqrt{x}$$

となります。ここで、$\sqrt{x}\geqq0$という正の平方根のとりうる値の範囲があるので、共通範囲は

$$\sqrt{x}>3$$

となります。
両辺が$0$以上であれば両辺を2乗しても大小関係は変わらないので$x$の範囲は

$$x>9$$

となります。

2.の方法

　$(t+5)(t-3)>0$、すなわち$(\sqrt{x}+5)(\sqrt{x}-3)>0$より$(\sqrt{x}+5)(\sqrt{x}-3)$は正の数となります。

掛けて正になる条件は$正×正=正,負×負=正$より

$$\begin{gather*}\left\{\begin{aligned}\sqrt{x}+5&>0\\[1em]\sqrt{x}-3&>0\end{aligned}\right.\tag{g}\\ \text{or}\\ \left\{\begin{aligned}\sqrt{x}+5&<0\\[1em]\sqrt{x}-3&<0\end{aligned}\right.\tag{h}\end{gather*}$$

となります。

ここで、$\sqrt{x}\geqq0$より$\sqrt{x}+5$は常に正となることがわかるので、$\text{(h)}$の$\sqrt{x}+5<0$は成り立たず不適となり$\text{(g)}$に絞り込まれます。

$\text{(g)}$の

$$\begin{align*}\sqrt{x}-3&>0\\[0.5em]\sqrt{x}&>3\end{align*}$$

と両辺が$0$以上であれば両辺を2乗しても大小関係は変わらないことから$x$の範囲は

$$x>9$$

となります。

関連：2次方程式のように解く方程式