x^2の係数が1でない2次式を工夫して因数分解する

\[\large 6x^2+7x-3\]

　上のように$x^2$の係数が$1$でない2次式を因数分解するのは、$x^2$の係数が$1$の2次式を因数分解するより少々面倒に感じます。

これを工夫して少し簡単に因数分解してみます。

　まずは$x^2$の係数$6$を定数項$-3$に移して掛け合わせます。
$x^2$の係数が$1$の2次式になるので、これを因数分解します。

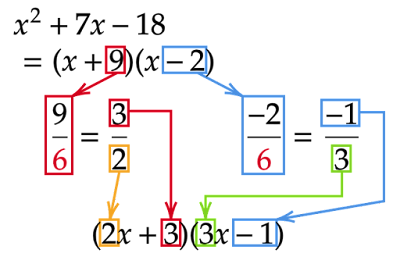
\[x^2+7x-18=(x+9)(x-2)\]

それぞれの因数の定数項を元々の2次式の$x^2$の係数$6$で割ります。

因数$x+9$の定数項$9$を$6$で割ると$\dfrac{3}{2}$となるので、分子の$3$を定数項に残して分母の$2$を$x$の係数に移すと$2x+3$になります。
また、因数$x-2$の定数項$-2$を$6$で割ると$\dfrac{-1}{3}$となるので、分子の$-1$を定数項に残して分母の$3$を$x$の係数に移すと$3x-1$になります。
ここで注意点があり、上のように定数項が負の数の場合はマイナスは分子に付け、割る数である$x^2$の係数が負の数の場合はマイナスは分母に付けます。

これら変形した因数同士の積$(2x+3)(3x-1)$が$6x^2-7x-3$を因数分解した形となります。

\[6x^2+7x-3=(2x+3)(3x-1)\]

　これがどんな2次式でもこの因数分解法が使えることを確かめてみます。

$x^2$が$1$でない2次式の因数分解は一般に

\begin{equation}\begin{aligned}acx^2+(ad+bc)x+bd&=(ax+b)(cx+d)\\ &(a,b,c,d:定数)\end{aligned}\end{equation}

という形になります。

次に$x^2$の係数$ac$を定数項へ移し、掛け合わせたものの因数分解は

\begin{equation}x^2+(ad+bc)x+abcd=(x+bc)(x+ad)\end{equation}

となります。

この2つの式を比較すると

$(2)$の2次式の因数$x+bc$の定数項$bc$を$(1)$の$x^2$の係数$ac$で割ると$\dfrac{b}{a}$です。
分子の$b$を残し分母の$a$を$x$の係数に移すと$ax+b$になります。

$(2)$の2次式の因数$x+ad$の定数項$ad$を$(1)$の$x^2$の係数$ac$で割ると$\dfrac{d}{c}$です。
分子の$d$を残し分母の$c$を$x$の係数に移すと$cx+d$になります。

したがって、$(1)$の右辺に直すことができます。

このようにどんな2次式においても、この因数分解法が使えることがわかります。

参考：FASTEST way to factor a trinomial! #shorts - YouTube

関連：$x^2$の係数が$1$の2次式の因数分解はどうやる？

関連：$x^2$の係数が$1$以外の2次式の因数分解はどうやる？