半径と同じ長さの弦に対する円周角は何度？

タレスの定理によると直径に対する円周角は直角となります。

では半径と同じ長さの弦に対する円周角は何度になるのでしょうか？

関連：タレスの定理とその逆

　半径と同じ長さの弦$\text{AB}$に対する円周角をつくる1辺が直径となるように点$\text{C}$をおきます。

円周角の定理より頂点が弦の同じ側にある限り円周角は一定となります。

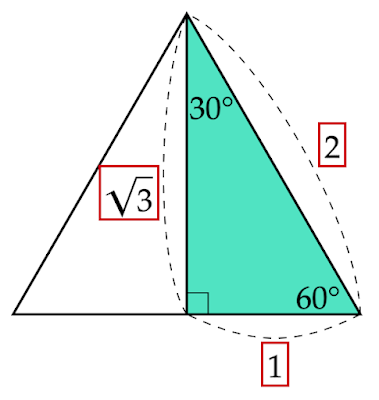
すると、タレスの定理より直径に対する円周角は直角なので、上図のように直角三角形ができます。

また、斜辺$\text{AC}$の長さが直径、$\text{AB}$の長さが半径なので、この2辺の比は$2:1$となります。

このような2辺の比を持つ直角三角形は内角が$30°-60°-90°$の直角三角形で、斜辺の半分の長さの辺の対角の大きさは$30°$です。

したがって、半径と同じ長さの弦に対する円周角は$30°$であるとわかります。

　半径と同じ長さの弦に対する円周角はもう1つあります。
弦$\text{AB}$を挟んで$30°$の円周角とは反対側にある円周角です。

上図のように点$\text{C}$を含まない方の弧$\text{AB}$上に点$\text{P}$をおくと四角形$\text{APBC}$ができます。

円に内接する四角形の対角の和は$180°$であるため、$∠\text{ACB}=30°$ならばもう1つの弦$\text{AB}$に対する円周角$∠\text{APB}$は$150°$となります。

　以上より、半径と同じ長さの弦に対する円周角は$30°$と$150°$となります。

関連：円周角の定理　なぜ成り立つのか？

関連：円に内接する四角形の対角