2円の異なる2つの交点を通る直線と2つの中心を通る直線の関係

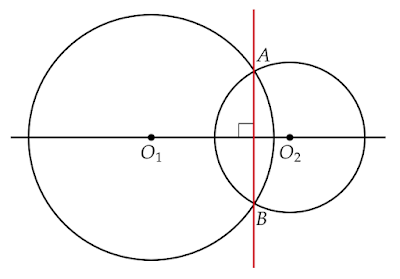
　2つの円の異なる2つの交点を通る直線は、2つの円の中心を通る直線に対し垂直になります。

なぜこのようなことが言えるのでしょうか？

　2つの円$\text{O$_1$, O$_2$}$が異なる2つの点$\text{A, B}$で交わっているとき、$△\text{AO$_1$O$_2$}, △\text{BO$_1$O$_2$}$について考えます。

$\text{O$_1$A, O$_1$B}$は円$\text{O$_1$}$の半径であるため$\text{O$_1$A}=\text{O$_1$B}$です。…(1)

同様に$\text{O$_2$A, O$_2$B}$は円$\text{O$_2$}$の半径であるため$\text{O$_2$A}=\text{O$_2$B}$です。

$\text{O$_1$O$_2$}$は共通な辺です。

3辺がそれぞれ等しいので$△\text{AO$_1$O$_2$}, △\text{BO$_1$O$_2$}$は合同であることがわかります。

このことから$∠\text{AO$_1$O$_2$}=∠\text{BO$_1$O$_2$}$です。…(2)

点$\text{A, B}$から直線$\text{O$_1$O$_2$}$に垂線を下ろし、その足をそれぞれ点$\text{C, C'}$とします。$\text{C}$と$\text{C'}$に分けるのは直線$\text{AB}$が直線$\text{O$_1$O$_2$}$に対し垂直でないと仮定するためです。

$△\text{AO$_1$C}, △\text{BO$_1$C'}$について考えると$\text{AC}\perp \text{O$_1$O$_2$}, \text{AC'}\perp \text{O$_1$O$_2$}$より、2つの三角形は直角三角形です。
(1)、(2)より、直角三角形の斜辺と鋭角の1つがそれぞれ等しいので$△\text{AO$_1$C}, △\text{BO$_1$C'}$は合同であることがわかります。
このことから$\text{O$_1$C}=\text{O$_1$C'}$です。

$△\text{AO$_2$C}, △\text{BO$_2$C'}$も同様に合同であることを示せるので、$\text{O$_2$C}=\text{O$_2$C'}$であることがわかります。

これはつまり、2点$\text{C, C'}$は直線$\text{O$_1$O$_2$}$上の$\text{O$_1$, O$_2$}$それぞれからの距離が等しい点であるということなので$\text{C, C'}$は同一の点であることがわかります。
したがって、$\text{A, C, B}$は同一直線$\text{AB}$上にあり、直線$\text{AB}$は直線$\text{O$_1$O$_2$}$に対し垂直であることがわかります。

　また、2円が外接・内接しているときも共通接線は2円の中心を通る直線に対して垂直になります。

これは以下のように確かめられます。

円$\text{O$_1$}$において点$\text{P}$における接線$l$は半径$\text{O$_1$P}$に対し垂直です。
円$\text{O$_2$}$において点$\text{Q}$における接線$m$は半径$\text{O$_2$Q}$に対し垂直です。

点$\text{P}$と$\text{Q}$、直線$l$と$m$が重なるように2円を移動させると直線$l\ (m)$は$\text{O$_1$P}$と$\text{O$_2$P}\ (\text{O$_2$Q})$に対して垂直となります。このとき$∠\text{O$_1$PO$_2$}$は$0°$または$180°$なので3点$\text{O$_1$, O$_2$, P}$は同一直線上にあります。

よって、2円$\text{O$_1$, O$_2$}$が点$\text{P}$で外接または内接しているとき、共通接線$m$は直線$\text{O$_1$O$_2$}$に対し垂直となることがわかります。