三角形の1辺の長さと両端の角から外接円の半径を求める

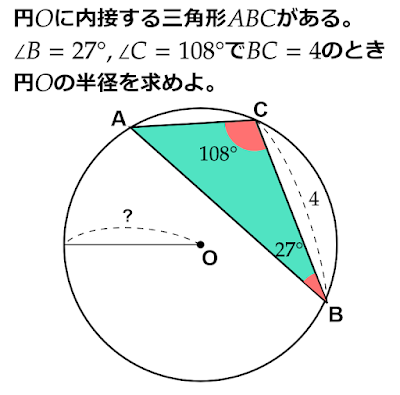
「円$\text{O}$に内接する$△\text{ABC}$がある。
$\text{BC}=4,∠\text{B}=27°,∠\text{C}=108°$のとき、円$\text{O}$の半径を求めよ。」

　まずは$∠\text{A}$を求めます。
三角形の内角の和は$180°$なので、

$$\begin{align*}∠\text{A}+27°+108°&=180°\\[0.5em]∠\text{A}&=180°-(27°+108°)\\[0.5em]&=180°-135°\\[0.5em]&=45°\end{align*}$$

となります。

正弦定理より

$$\frac{\text{BC}}{\sin∠\text{A}}=2R\quad(R:\text{外接円の半径})$$

なので、

$$\begin{align*}\frac{4}{\sin45°}&=2R\\[0.5em]\frac{4}{\cfrac{\sqrt{2}}{2}}&=2R\\[0.5em]\frac{8}{\sqrt{2}}&=2R\\[0.5em]R&=\frac{4}{\sqrt{2}}\\[0.5em]&=\frac{4\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}\\[0.5em]&=\frac{4\sqrt{2}}{2}\\[0.5em]&=2\sqrt{2}\end{align*}$$

となります。

　正弦定理というと上図より

$$\frac{a}{\sin∠\text{A}}=\frac{b}{\sin∠\text{B}}=\frac{c}{\sin∠\text{C}}$$

という1辺とその対角による関係に目が行きがちですが、定理の全体は

$$\frac{a}{\sin∠\text{A}}=\frac{b}{\sin∠\text{B}}=\frac{c}{\sin∠\text{C}}=2R$$

で、外接円の半径（または直径）とも関係する定理となっています。

関連：正弦定理　なぜ成り立つ？

関連：円に内接する三角形の1辺の長さは？