絶対値を含む1次不等式を解く(2)

「次の不等式を解け。

(1)$|x-1|>2x-1$

(2)$|x+1|\leqq-\dfrac{1}{2}x+1$」

　このような問題はどのように解けばよいでしょうか？

　絶対値の中身と外側に$x$が含まれる不等式は絶対値記号を外したときの結果によって場合分けをします。

(1)$|x-1|>2x-1$

　絶対値記号を外したときの結果とその時の$x$の条件は以下のようになります。

$$\begin{align*}x<1のとき\\ |x-1|&=-(x-1)=-x+1\\[0.5em]x\geqq1のとき\\ |x-1|&=x-1\end{align*}$$

これをもとに不等式を解きます。

$x<1$のとき

$$\begin{align*}-x+1&>2x-1\\[0.5em]3x&<2\\[0.5em]x&<\frac{2}{3}\end{align*}$$
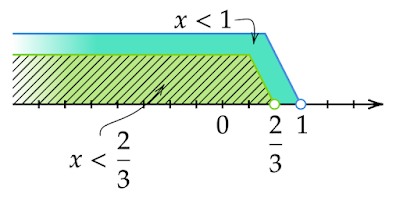
条件$x<1$と解$x<\dfrac{2}{3}$を同時に満たしている、すなわち数直線で範囲を表したとき共通している部分が不等式の解となります。

数直線より解の1つは$x<\dfrac{2}{3}$となります。

$x\geqq1$のとき

$$\begin{align*}x-1&>2x-1\\[0.5em]x&<0\end{align*}$$

条件$x\geqq1$と$x<0$では共通している部分がないので、この条件下では解なしとなります。

以上から、この不等式の解は$x<\dfrac{2}{3}$となります。

(2)$|x+1|\leqq-\tfrac{1}{2}x+1$

　(1)と同様に解きます。

$$\begin{align*}x<-1のとき\\ |x+1|&=-(x+1)=-x-1\\[0.5em]x\geqq-1のとき\\ |x+1|&=x+1\end{align*}$$

なので、

$x<-1$のとき

$$\begin{align*}-x-1&\leqq-\frac{1}{2}x+1\\[0.5em]\frac{1}{2}x&\geqq-2\\[0.5em]x&\geqq-4\end{align*}$$
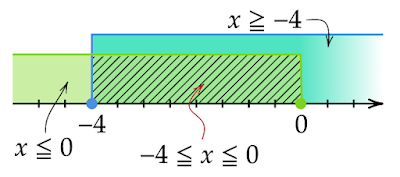
条件$x<-1$と解$x\geqq-4$の共通している部分を調べると

数直線より解の1つは$-4\leqq x<-1$となります。

$x\geqq-1$のとき

$$\begin{align*}x+1&\leqq-\frac{1}{2}x+1\\[0.5em]\frac{3}{2}x&\leqq0\\[0.5em]x&\leqq0\end{align*}$$

条件$x\geqq-1$と解$x\leqq0$の共通している部分を調べると

数直線より解の1つは$-1\leqq x\leqq0$となります。

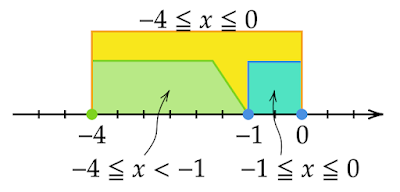
以上から、この不等式の解は$-4\leqq x<-1$または$-1\leqq x\leqq0$となりますが、この2つの範囲内にある$-4$から$0$まで$x$を変化させてみると必ずどちらかの範囲を満たして途切れることがありません。

このとき、2つの範囲をまとめて$-4\leqq x\leqq0$と書くことができます。したがって、これがこの不等式の解となります。

関連：絶対値を含む1次不等式を解く(1)

上のリンクのような解き方で解くこともできます。

(1)

　これは

$$\begin{align*}|x|&>A\\[0.5em]x<-A&,A<x\end{align*}$$

とできる形であるから

\begin{align*}|x-1|&>2x-1\\ \\ x-1<-2x+1,&2x-1<x-1\\[0.5em]3x<2,&x<0\\[0.5em]x<\frac{2}{3},&x<0\end{align*}

$x<\dfrac{2}{3}$か$x<0$のどちらかを必ず満たしていればよいということだから、

数直線より$x<\dfrac{2}{3}$だけで事足りるので、これが不等式の解となります。

(2)

　これは

$$\begin{align*}|x|&\leqq A\\[0.5em]-A\leqq &x\leqq A\end{align*}$$

とできる形であるから

$$\begin{align*}|x+1|&\leqq-\frac{1}{2}x+1\\[0.5em]\frac{1}{2}x-1\leqq &x+1\leqq -\frac{1}{2}x+1&\cdots(*)\end{align*}$$

この不等式は

$$\left\{\begin{aligned}\frac{1}{2}x-1&\leqq x+1&\cdots(a)\\[0.5em]x+1&\leqq -\frac{1}{2}x+1&\cdots(b)\end{aligned}\right.$$

と分けることができるから、それぞれ解いて

$$\begin{align*}(a)\ \frac{1}{2}x-1&\leqq x+1\\[0.5em]\frac{1}{2}x&\geqq-2\\[0.5em]x&\geqq-4&\cdots(c)\\[1.5em](b)\ x+1&\leqq -\frac{1}{2}x+1\\[0.5em]\frac{3}{2}x&\leqq0\\[0.5em]x&\leqq0&\cdots(d)\end{align*}$$

(*)は(a)と(b)を同時に満たしている不等式なので、(c)と(d)もまた同時に満たしているものが解となります。

したがって、(c)、(d)の共通する範囲が不等式の解なので$-4\leqq x\leqq0$となります。