なぜ複素数は|a+bi|^2=(a+bi)^2とすることができないのか？

　実数$a,b$について
$$|a+b|^2=(a+b)^2$$
という式が成り立ちます。しかし、複素数$a+bi$の場合だと
$$|a+bi|^2=(a+bi)(a-bi)$$
となります。

なぜ、複素数の場合

$$|a+bi|^2=(a+bi)^2$$

ではないのでしょうか？

　$|a+b|^2=(a+b)^2$が成立するのは、

$$\begin{align*}a+b<0のとき\\ |a+b|&=-(a+b)\\[1.5em]a+b\geqq0のとき\\ |a+b|&=a+b\end{align*}$$

より

$$\begin{align*}a+b<0のとき\\ |a+b|^2&=\left\{-(a+b)\right\}^2\\[0.5em]&=(a+b)^2\\[1.5em]a+b\geqq0のとき\\ |a+b|^2&=(a+b)^2\end{align*}$$

となり、実数$a+b$の正負で場合分けしても同じ結果を得るためです。

$|a+bi|$を実数と同様に場合分けしようとした場合、$b=0$のとき$a+bi$は実数なので場合分けができて結果成り立つことがわかります。しかし$b\neq0$のとき$a+bi$は虚数となり、虚数には大きさがない、すなわち虚数を$0$未満か$0$以上かで場合分けすることができないので、実数と同じ方法はとれなくなります。

　では複素数の絶対値$|a+bi|$はどうやって求めるのかというと、これは複素数平面で定義されています。

平面上に互いに垂直な数直線、実軸$Re$と虚軸$Im$をおきます。この平面を複素数平面といいます。

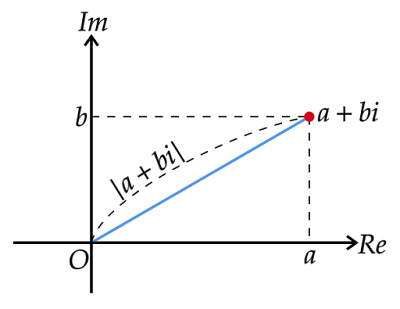
実部$a$と虚部$b$は実軸、虚軸それぞれにおける座標となるので、座標平面でいうところの$(a,b)$の点が複素数$a+bi$の複素数平面における位置となります。

そして原点から$a+bi$までの距離が複素数の絶対値$|a+bi|$となります。実数の絶対値は実数直線における$0$点からの距離なので、これを拡張したものです。

したがって、三平方の定理を利用して

$$|a+bi|^2=a^2+b^2$$

で求めることができます。

ここで、

$$\begin{align*}(a+bi)^2&=a^2+2abi+b^2i^2\\[0.5em]&=a^2-b^2+2abi\end{align*}$$

より$|a+bi|^2=(a+bi)^2$が成り立たないことがわかります。

　複素数平面を利用して複素数の絶対値を求める方法はわかりましたが、なぜ
$$|a+bi|^2=(a+bi)(a-bi)$$
となるのかはまだわかりません。そこで$a^2+b^2$と$(a+bi)^2$を比較して導いてみます。

$(a+bi)^2=a^2-b^2+2abi$より、これを$a^2+b^2$にするには$2abi$を引いて$2b^2$を加える必要があります。

$$\begin{align*}a^2+b^2&=(a+bi)^2-2abi+2b^2\\[0.5em]&=(a+bi)^2-2b(ai-b)\\[0.5em]&=(a+bi)^2-2b(ai+bi^2)\\[0.5em]&=(a+bi)^2-2bi(a+bi)\\[0.5em]&=(a+bi){(a+bi)-2bi}\\[0.5em]&=(a+bi)(a-bi)\end{align*}$$

このことから$|a+bi|^2=(a+bi)(a-bi)$を導くことができました。

このとき複素数$a+bi$に対する$a-bi$、すなわち虚部の符号が反転している複素数のことを共役複素数と呼びます。

共役複素数$a-bi$は複素数平面において$a+bi$をx軸に関して対称な位置にあります。