連立方程式をグラフで考える

　連立方程式をグラフで考えるとどうなるのでしょうか？

　連立方程式は複数の方程式を同時に成り立たせるような共通する$x,y$の値の組があるという考えからつくられます。この$x,y$の値の組とは平面上においては座標のことです。
したがって、連立方程式の解とは連立されている方程式が描く図形の交点（より広い意味では共有点）の座標を表すことになります。

　例として連立方程式

\[\left\{\begin{array}{rlr}3x+y&=9&\cdots\text{(a)}\\[0.5em]2x+5y&=19&\cdots\text{(b)}\end{aligned}\right.\]

について考えます。

$\text{(a)}$を変形すると

\begin{align*}3x+y&=9\\[0.5em]y&=-3x+9\end{align*}

$\text{(b)}$を変形すると

\begin{align*}2x+5y&=19\\[0.5em]5y&=-2x+19\\[0.5em]y&=-\frac{2}{5}x+\frac{19}{5}\end{align*}

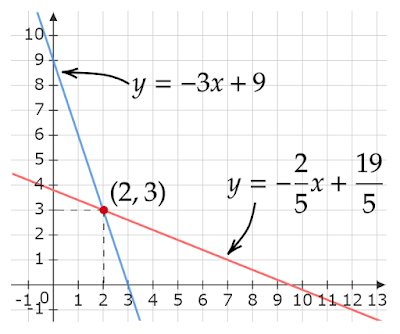
となり、これらのグラフは

のようにどちらも直線になります。

それぞれの方程式で表される直線は、方程式を成り立たせることができる$(x,y)$の点の集まりです。したがって、直線の交点は2つの方程式を同時に成り立たせることができる$(x,y)$、すなわち連立方程式の解であることがわかります。

例の連立方程式の中の方程式はグラフでは$(2,3)$で交わるので、連立方程式の解は$(x,y)=(2,3)$となります。

　2つの直線の方程式を連立したとき2直線の交点は1つだけなので、このときの連立方程式の解も1つだけとなります。連立方程式の解の個数はどんな図形の方程式を連立したかで変わります。

　2つの直線の方程式を連立したとき、ただ1つの解を持たない場合があります。今度はその場合を見てみます。

　連立方程式

\begin{cases}3x+y=17\\[0.5em]3x+y=9\end{cases}

を例にすると、それぞれの方程式を$y$について解くと

\begin{cases}y=-3x+17\\[0.5em]y=-3x+9\end{cases}

となり、これらのグラフは

のようになります。

これらの直線の方程式は傾きが等しくy切片が異なるため、2直線は平行であることがわかります。平行であるということは交点がないということなので、平行な直線の方程式を連立したときその解は存在しません。

　次は連立方程式

\[\left\{\begin{aligned}6x+2y&=18\\[0.5em]3x+y&=9\end{aligned}\right.\]

について考えます。

これらを変形するとどちらも

\[y=-3x+9\]

になります。

すなわち同じ直線を表すため、この直線上の点$(x,y)$すべてが共有点となります。

したがって、このときの連立方程式の解の個数は無数にあります。

関連：連立方程式を解く