2次関数の頂点が最大・最小となる条件

「2次関数$y=ax^2+2a^2x-5$ $(-2\leqq x\leqq3,\ a:実数)$において以下を満たすような$a$の値の範囲を求めよ。

(1)頂点で最大となる。

(2)頂点で最小となる。」

このような問題はどのように解けばよいでしょうか？

　最大値・最小値に関連する問題なので、まずは平方完成します。

$$\begin{align*}y&=ax^2+2a^2x-5\\[0.5em]&=a(x^2+2ax)-5\\[0.5em]&=a\{(x+a)^2-a^2\}-5\\[0.5em]y&=a(x+a)^2-a^3-5\end{align*}$$

このことから軸の方程式は$x=-a$、頂点の座標は$(-a,-a^3-5)$となります。

関連：平方完成するには

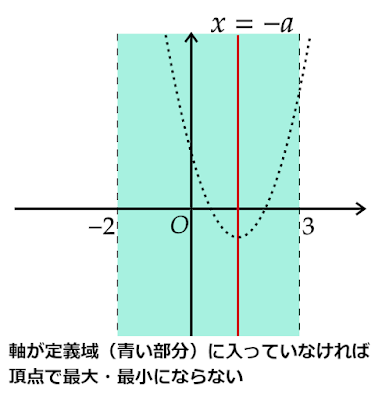
軸が定義域内にないと頂点も定義域内にないので頂点で最大・最小になることはありません。したがって、頂点が定義域内にあるための$a$の範囲は$-2\leqq-a\leqq3$、すなわち$-3\leqq a\leqq2$となります。

また、2次関数であるためには$a\neq0$でなければならないので$a$の範囲は$-2\leqq a<0,0<a\leqq3$の2つにわかれます。

　それぞれの$a$の範囲について見ていくと、

$-3\leqq a<0$のときは$a$が負なので$x^2$の係数も負となり、上に凸の放物線を描くから頂点で最大となります。

$0<a\leqq2$のときは$a$が正なので$x^2$の係数も正となり、下に凸の放物線を描くから頂点で最小となります。

　したがって、問題の答えは

(1)$-3\leqq a<0$

(2)$0<a\leqq2$

となります。

関連：2次関数の最大値・最小値を求める