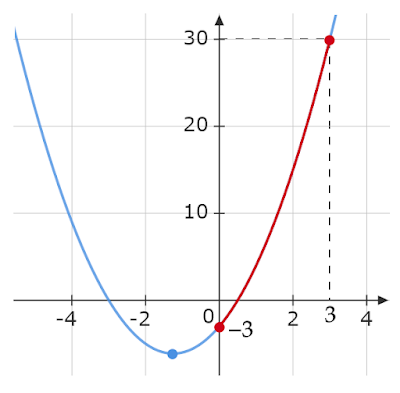
1. $y=2x^2+5x-3$
①$-2\leqq x\leqq1$ ②$0\leqq x\leqq3$
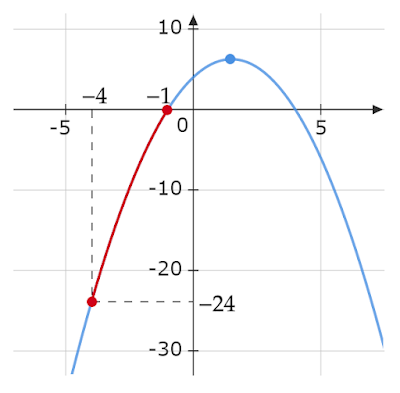
2. $y=-x^2+3x+4$
①$-4\leqq x\leqq-1$ ②$1\leqq x\leqq3$」
このような問題はどのように考えればよいでしょうか？
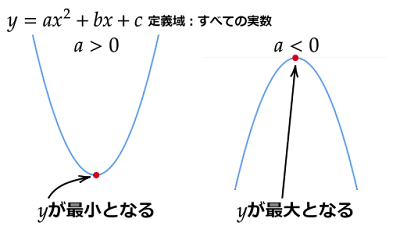
2次関数は放物線を描くので、すべての実数を定義域とするとき必ず$y$は頂点で最大値または最小値となります。
定義域における2次関数の最大値と最小値を求めるときは、頂点のx座標が定義域に含まれているかどうかで求め方が変わります。
なので、まずは頂点の座標を知るために平方完成を行います。
1. $y=2x^2+5x-3$
\begin{align*}2x^2+5x-3&=2\left(x^2+\frac{5}{2}x\right)-3\\[0.5em]&=2\left(x^2+\frac{5}{2}x+\frac{25}{16}-\frac{25}{16}\right)-3\\[0.5em]&=2\left(x^2+\frac{5}{2}x+\frac{25}{16}\right)-\frac{25}{8}-3\\[0.5em]&=2\left(x+\frac{5}{4}\right)^2-\frac{49}{8}\end{align*}
となるので、頂点の座標は$\left(-\dfrac{5}{4},-\dfrac{49}{8}\right)$であるとわかります。
2. $y=-x^2+3x+4$
\begin{align*}-x^2+3x+4&=-(x^2-3x)+4\\[0.5em]&=-\left(x^2-3x+\frac{9}{4}\right)+\frac{9}{4}+4\\[0.5em]&=-\left(x-\frac{3}{2}\right)^2+\frac{25}{4}\end{align*}
となるので、頂点の座標は$\left(\dfrac{3}{2},\dfrac{25}{4}\right)$であるとわかります。
次は頂点と定義域の位置関係について考えます。
.png)
.png)
- $a>0$のとき、頂点において$y$は最小値をとります。$y$が最大値をとるのは定義域の端のどちらかです。
- $a<0$のとき、頂点において$y$は最大値をとります。$y$が最小値をとるのは定義域の端のどちらかです。
以上を踏まえて問題を解きます。
1. $y=2x^2+5x-3$
2次関数$y=2x^2+5x-3$の頂点の座標は$\left(-\dfrac{5}{4},-\dfrac{49}{8}\right)$です。
①$-2\leqq x\leqq1$
定義域が$-2\leqq x\leqq1$のとき、頂点のx座標は定義域に含まれます。
定義域の端における$y$について調べると$x=-2$のとき$y=-5$、$x=1$のとき$y=4$なので、最大値は$x=1$のとき$4$
②$0\leqq x\leqq3$
定義域が$0\leqq x\leqq3$のとき、頂点のx座標は定義域に含まれません。
2. $y=-x^2+3x+4$
2次関数$y=-x^2+3x+4$の頂点の座標は$\left(\dfrac{3}{2},\dfrac{25}{4}\right)$です。
①$-4\leqq x\leqq-1$
定義域が$-4\leqq x\leqq-1$のとき、頂点のx座標は定義域に含まれません。
②$1\leqq x\leqq3$
定義域が$1\leqq x\leqq3$のとき、頂点のx座標は定義域に含まれます。
定義域の端におけるyについて調べると$x=1$のとき$y=6$、$x=3$のとき$y=4$なので、最小値は$x=3$のとき$4$
2次関数の最大値と最小値を求めるために頂点の座標と定義域の端におけるyの値をしっかり調べておくことが重要になります。
Share:
