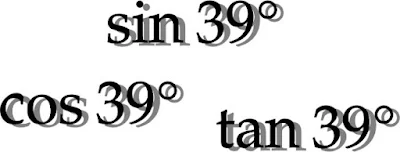$39°\ (=\dfrac{13\pi}{60})$のときの三角関数がどんな式で表されるのかを調べてみました。
$\sin39°$
$\sin$の加法定理より
\begin{align*}\sin39°&=\sin(24°+15°)\\[0.5em]&=\sin24°\cos15°+\cos24°\sin15°\end{align*}
「$\sin15°,\cos15°,\tan15°$はどんな数?」、「$\sin24°,\cos24°,\tan24°$はどんな数?」より
\begin{align*}\sin15°&=\frac{\sqrt{2}(\sqrt{3}-1)}{4}\\[0.5em]\cos15°&=\frac{\sqrt{2}(\sqrt{3}+1)}{4}\\[1em]\sin24°&=\frac{\sqrt{3}(\sqrt{5}+1)-\sqrt{10-2\sqrt{5}}}{8}\\[0.5em]\cos24°&=\frac{(\sqrt{5}+1)+\sqrt{3}\sqrt{10-2\sqrt{5}}}{8}\end{align*}
なので、
\begin{align*}\sin39°&=\frac{\sqrt{3}(\sqrt{5}+1)-\sqrt{10-2\sqrt{5}}}{8}\cdot\frac{\sqrt{2}(\sqrt{3}+1)}{4}\\
&\qquad+\frac{(\sqrt{5}+1)+\sqrt{3}\sqrt{10-2\sqrt{5}}}{8}\cdot\frac{\sqrt{2}(\sqrt{3}-1)}{4}\\[0.5em]&=\frac{\sqrt{2}\{(\sqrt{3}+1)(\sqrt{5}+1)-(\sqrt{3}-1)\sqrt{10-2\sqrt{5}}\}}{16}\tag{a}\\[0.5em]&=\underline{\frac{\sqrt{2}+\sqrt{6}+\sqrt{10}+\sqrt{30}-2\sqrt{20-10\sqrt{3}-4\sqrt{5}+2\sqrt{15}}}{16}}\end{align*}
$\cos39°$
$\cos$の加法定理より
\begin{align*}\cos39°&=\cos(24°+15°)\\[0.5em]&=\cos24°\cos15°-\sin24°\sin15°\\[0.5em]&=\frac{(\sqrt{5}+1)+\sqrt{3}\sqrt{10-2\sqrt{5}}}{8}\cdot\frac{\sqrt{2}(\sqrt{3}+1)}{4}\\
&\qquad-\frac{\sqrt{3}(\sqrt{5}+1)-\sqrt{10-2\sqrt{5}}}{8}\cdot\frac{\sqrt{2}(\sqrt{3}-1)}{4}\\[0.5em]&=\frac{\sqrt{2}\{(\sqrt{3}-1)(\sqrt{5}+1)+(\sqrt{3}+1)\sqrt{10-2\sqrt{5}}\}}{16}\tag{b}\\[0.5em]&=\underline{\frac{2\sqrt{20+10\sqrt{3}-4\sqrt{5}-2\sqrt{15}}-\sqrt{2}+\sqrt{6}-\sqrt{10}+\sqrt{30}}{16}}\end{align*}
$\tan39°$
三角関数の相互関係
\[\tan\theta=\frac{\sin\theta}{\cos\theta}\]
より、$\text{(a),(b)}$を代入して
\begin{align*}\tan39°&=\frac{\sin39°}{\cos39°}\\[0.5em]&=\frac{\cfrac{\sqrt{2}\{(\sqrt{3}+1)(\sqrt{5}+1)-(\sqrt{3}-1)\sqrt{10-2\sqrt{5}}\}}{16}}{\cfrac{\sqrt{2}\{(\sqrt{3}-1)(\sqrt{5}+1)+(\sqrt{3}+1)\sqrt{10-2\sqrt{5}}\}}{16}}\\[0.5em]&=\frac{(\sqrt{3}+1)(\sqrt{5}+1)-(\sqrt{3}-1)\sqrt{10-2\sqrt{5}}}{(\sqrt{3}-1)(\sqrt{5}+1)+(\sqrt{3}+1)\sqrt{10-2\sqrt{5}}}\\
&\qquad×\frac{(\sqrt{3}-1)(\sqrt{5}+1)-(\sqrt{3}+1)\sqrt{10-2\sqrt{5}}}{(\sqrt{3}-1)(\sqrt{5}+1)-(\sqrt{3}+1)\sqrt{10-2\sqrt{5}}}\\[0.5em]&=\frac{(\sqrt{5}+1)\sqrt{10-2\sqrt{5}}-4}{2\{2\sqrt{3}-(\sqrt{5}-1)\}}×\frac{2\sqrt{3}+(\sqrt{5}-1)}{2\sqrt{3}+(\sqrt{5}-1)}\\[0.5em]&=\frac{(2+\sqrt{3}+\sqrt{15})\sqrt{10-2\sqrt{5}}-2(2\sqrt{3}+\sqrt{5}-1)}{2(3+\sqrt{5})}×\frac{3-\sqrt{5}}{3-\sqrt{5}}\\[0.5em]&=\frac{(3-\sqrt{3}-\sqrt{5}+\sqrt{15})\sqrt{10-2\sqrt{5}}+2(4-3\sqrt{3}-2\sqrt{5}+\sqrt{15})}{4}\\[0.5em]&=\frac{\sqrt{(3-\sqrt{3}-\sqrt{5}+\sqrt{15})^2(10-2\sqrt{5})}+2(4-3\sqrt{3}-2\sqrt{5}+\sqrt{15})}{4}\\[0.5em]&=\underline{\frac{\sqrt{110-60\sqrt{3}-46\sqrt{5}+28\sqrt{15}}+4-3\sqrt{3}-2\sqrt{5}+\sqrt{15}}{2}}\end{align*}
それぞれの近似値は以下のようになります。
\begin{align*}\sin39°&=0.62932\\[1em]\cos39°&=0.77715\\[1em]\tan39°&=0.80978\end{align*}
Share: