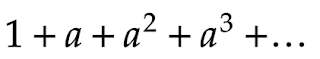$1+a+a^2+a^3+\ldots$と延々と続く式の因数分解をするにはどうすればよいでしょうか?
まずは、項の数を少なくして$1+a+a^2+a^3$の因数分解をしてみます。
\begin{align*}1+a+a^2+a^3&=(1+a)+(a^2+a^3)\\[0.5em]&=(1+a)+a^2(1+a)\\[0.5em]&=\underline{(1+a)(1+a^2)}\end{align*}
これを利用して$1+a+a^2+a^3+\ldots$の因数分解をします。
\begin{align*}1+a+a^2+a^3+a^4+a^5+\ldots&=(1+a)+(a^2+a^3)+(a^4+a^5)+\ldots\\[0.5em]&=(1+a)+a^2(1+a)+a^4(1+a)+\ldots\\ &=(1+a)(1+a^2+a^4+a^6+\ldots)\\[0.5em]&=(1+a)\{(1+a^2)+(a^4+a^6)+\ldots\}\\[0.5em]&=(1+a)\{(1+a^2)+a^4(1+a^2)+\ldots\}\\[0.5em]&=(1+a)(1+a^2)(1+a^4+a^8+a^{12}+\ldots)\\ &\qquad\vdots\\
&=\underline{(1+a)(1+a^2)(1+a^4)(1+a^8)\ldots}\end{align*}
というように因数分解をすることができます。
ちなみに$1+a+a^2+a^3+\ldots$というのは、初項$1$、公比$a$の等比数列の和(無限等比級数)です。
項数が有限かつ$a\neq1$である場合は等比数列の和
\[\frac{a^n-1}{a-1}\quad(n:1の項も含めた項数)\]
を利用して因数分解できます。
因数分解した式は総乗をもちいると
\[\prod_{k=1}^\infty{(1+a^{2^{k-1}})}\]
と書けます。
Share: