2次不等式を解く

上の2次不等式を解くとき、どのように考えればよいでしょうか？

　この2次不等式は、$x^2+x-12$の値が$0$以下（0か負）になることを表しています。2次不等式を解くとは前述のような値を示すときの$x$の値の範囲はどうなるかということを求めるということです。

まず、2次方程式を解くときと同じく因数分解をします。

$$(x+4)(x-3)\leqq 0$$

このような式に変形すると、$x+4$と$x-3$という2つの数を掛けて$0$以下になる条件を調べることで2次不等式を解くことができます。

ここで、不等式が成り立つ条件は細かく分類すれば以下のようになります。

1. $A<0$かつ$B>0$のとき（負になる条件1）

例えば$A=-1,B=1$とすれば

$$-1× 1=-1<0$$

なので、$AB<0$を満たします。

2. $A>0$かつ$B<0$のとき（負になる条件2）

例えば$A=1,B=-1$とすれば

$$1× (-1)=-1<0$$

なので、$AB<0$を満たします。

3. $A<0$かつ$B<0$のとき（正になる条件1）

例えば$A=-1,B=-1$とすれば

$$-1×(-1)=1>0$$

なので、$AB>0$を満たします。

4. $A>0$かつ$B>0$のとき（正になる条件2）

例えば$A=1,B=1$とすれば

$$1×1=1>0$$

なので、$AB>0$を満たします。

5. $A=0$のとき（0になる条件1）

$$0× B=0$$

なので、$A× B\leqq 0$を満たします。
このとき、$B$のとる値は何でも構いません。

6. $B=0$のとき（0になる条件2）

$$A× 0=0$$

なので、$A× B\leqq 0$を満たします。
このとき、$A$のとる値は何でも構いません。

1.、2.は掛けて負になる条件、3.、4.は掛けて正になる条件です。これらの条件の元になるのは

$$\begin{align*}(正)×(正)&=(正)&(正)×(負)&=(負)\\ \\ (負)×(正)&=(負)&(負)×(負)&=(正)\end{align*}$$

という積の正負です。
5.、6.は等号付き不等号（$\leqq,\geqq$）の不等式のときだけの条件です。

ですが、等号付き不等号の不等式の場合も4つにまとめることができます。

1’. $A\leqq0$かつ$B\geqq0$の場合（0以下になる条件1）
2’. $A\geqq0$かつ$B\leqq0$の場合（0以下になる条件2）
3’. $A\leqq0$かつ$B\leqq0$の場合（0以上になる条件1）
4’. $A\geqq0$かつ$B\geqq0$の場合（0以上になる条件2）

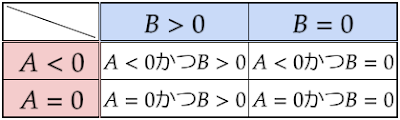
例えば1'.の条件は$A\leqq0$は$A<0$または$A=0$を表すものであることから、「『$A<0$または$A=0$』かつ『$B>0$または$B=0$』」と書くことができ、これは以下の表に表されるような条件の組み合わせをつくることができます。

1'.と対になる2'.でつくることができる条件と合わせると1.、2.、5.、6.に当てはまるときに考えられうるすべての条件の組み合わせとなります。これは3'.と4'.の場合も同様です。

　では、上記を踏まえ冒頭の2次不等式を解いてみると、$A=x+4,B=x-3$とおくと1'.、2'.が当てはまります。

1'.にあてはまるとき

$$\begin{align*}A=x+4&\leqq0\\[0.5em]x&\leqq-4\\[1.5em]B=x-3&\geqq0\\ \\ x&\geqq3\end{align*}$$

なので、$x\leqq-4かつx\geqq3$となります。
これは$x$は$-4$以下$3$以上の数である、ということです。

そのような数は存在しないので、これを満たす$x$の範囲も存在しません。

2'.にあてはまるとき

$$\begin{align*}A=x+4&\geqq0\\[0.5em]x\geqq-4\\[1.5em]B=x-3&\leqq0\\ \\ x&\leqq3\end{align*}$$

なので、$\mathbf{x\geqq-4かつx\leqq3}$となります。
これは$x$は$-4$以上$3$以下の数である、ということです。

したがって、この$x$の範囲は$-4\leqq x\geqq3$と書くことができます。

以上から$x^2+x-12\leqq 0$の解は$\mathbf{-4\leqq x\leqq 3}$となります。

　また、$y=x^2+x-12$のグラフを描き、$y\leqq 0$となっている部分から$x$の値の範囲を求めると直感的に解くことができます。この方法はどういったものを求めようとしているのかがわかりやすいです。

グラフを使った2次不等式の解き方は以下の記事で紹介します。

関連：2次不等式を解く(2)