すべての角が等しければ正多角形になるか？

　正多角形には、

• すべての角が等しい。
• すべての辺の長さが等しい。

という特徴があります。これらのうち、「すべての角が等しい」という特徴のみで正多角形であることを示すことはできるでしょうか？

正三角形の場合

　まずは正三角形について考えます。

正三角形の内角が変わらないように変形してみて正三角形以外の三角形にならないことを示せれば「すべての角が等しい」ことが正三角形の条件であると言えます。
内角が変わらないように変形するには、平行線の性質を利用して正三角形の1辺に平行な直線を引き、他の2辺を延長して別の三角形を作る方法があります。
この方法でできた三角形は正三角形でしょうか？

図1　正三角形の場合

　図1のように上記の方法で正三角形ABCの外側にBCに平行な直線を引くことで新たに三角形ADEを作りました。正三角形ABCの1辺ACの長さをa、三角形ADEの対応する1辺AEの長さをbとします。

相似条件より3組の角が等しいので△ABCと△ADEは相似です。
相似であるならば△ADEは正三角形ですが、さらに確かめてみるなら

\[AC:AE=a:b\]

で、これが相似比なので同様に

\[AB:AD=BC:DE=a:b\]

であり、△ABCは正三角形なのでAB=BC=aであるから、AD=DE=bとなります。

したがって、△ADEはすべての角が等しく、すべての辺が等しいため、確かに正三角形であることがわかります。

正方形の場合

　次は正方形について考えてみます。

正三角形のとき同様1つの辺に平行な線を引き、隣の2辺を延長して新たな四角形を作ってみます。

図2　正方形の場合

正方形ABCDの外側にCDに平行な直線を引き、新たに四角形ABEFをつくります。
正方形ABCDはすべての辺の長さが等しいですが、四角形ABEFはAF＝BEであるものの他の辺より長くなってしまっているため正方形ではなく長方形になっています。

したがって、四角形はすべての角が等しくても正方形になるとは限らないということです。

正五角形の場合

　正五角形の場合も見てみましょう。

図3　正五角形の場合

正五角形ABCDEの外側に1辺DEに平行な直線を引き、新たに五角形ABCFGをつくります。
五角形ABCFGのAB、BCと比べCF、AGは長く、FGは短いです。これでは五角形ABCFGは正五角形であるとは言えません。

したがって、すべての角が等しくても正五角形になるとは限らないことがわかります。

　正五角形以上の頂点の数の正多角形の場合も正五角形と同様に変形しても正多角形にはなりません。
正三角形の場合のみ変形しても相似条件を満たすため正三角形となります。

　では「すべての辺の長さが等しい」ならば正多角形なのかというと、

図4　ひし形

図5　凹五角形

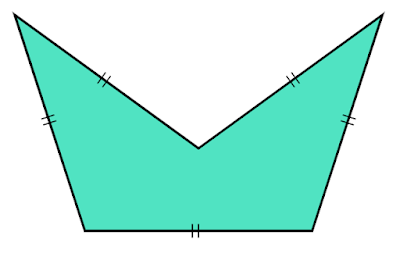
四角形であればひし形、五角形であれば図5のようなへこんだ部分のある五角形も該当するため、すべての辺の長さが等しいとしても正多角形であるとは限らないことがわかります。