外角の和はいくつになる？

外角とは

　外角とは、多角形の辺を延長することで図形の外側にできる角のことで、頂点は2つの辺でできるため1つの内角に対して2つの外角があります。

外角の性質は2つの外角は互いに対頂角となるため等しいことと外角1つと内角の和は

$$\begin{equation}\textbf{外角}+\textbf{内角}=180°\end{equation}$$

となることです。

多角形の内角の和は

　外角の和を求める前に、内角の和について考えます。

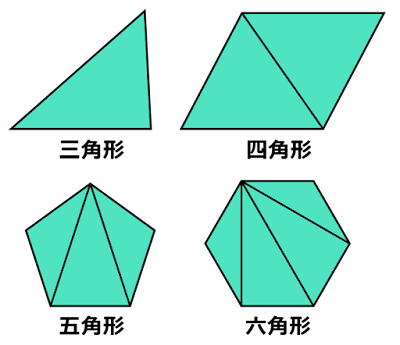
多角形は対角線同士が交わらないように引くと、いくつかの三角形に分割することができます。

対角線の引き方で簡単なのは、1つの頂点から他の頂点へ対角線を引くことです。
できる三角形の数は、三角形は1つとして、四角形は2つ、五角形は3つ、六角形は4つ、……と頂点の数が1つ増えるごとにできる三角形の数も1つ増えます。

このことから、できる三角形の数は

$$\textbf{三角形の数}=\textbf{頂点の数}-2$$

であることがわかります。

三角形に分割するときに多角形の頂点以外の頂点を作らなかったので、多角形の内角の和を三角形の数を利用して表すことができます。三角形の内角の和は$180°$なので

$$\begin{equation}\begin{aligned}\textbf{内角の和}&=180°×\textbf{三角形の数}\\[0.5em]&=180°(\textbf{頂点の数}-2)\end{aligned}\end{equation}$$

となります。

外角の和は

　外角の和を1つの内角につき2つある外角のうちの片方だけの合計であるとすると、内角と外角はそれぞれ多角形の頂点の数だけ存在するので、$n$角形の頂点にそれぞれ$1,2,\cdots,n$と番号を振ると$(1)$より

$$\begin{align*}\textbf{外角1}+\textbf{内角1}&=180°\\[0.5em]\textbf{外角2}+\textbf{内角2}&=180°\\ \vdots\quad\qquad\vdots\quad&\qquad\vdots\\ \textbf{外角n}+\textbf{内角n}&=180°\end{align*}$$

これらの辺々を加えると上の式は頂点の数だけあるので

$$\begin{align*}&(\textbf{外角1}+\textbf{外角2}+\cdots+\textbf{外角n})\\ &\quad+(\textbf{内角1}+\textbf{内角2}+\cdots+\textbf{内角n})=180°×\textbf{頂点の数}\end{align*}$$

となります。外角同士の和の部分を外角の和、内角同士の和の部分を内角の和と書き換えると、

$$\textbf{外角の和}+\textbf{内角の和}=180°×\textbf{頂点の数}$$

$(2)$より

$$\begin{align*}\textbf{外角の和}+\{180°(\textbf{頂点の数}-2)\}&=180°×\textbf{頂点の数}\\[0.5em]\textbf{外角の和}+(180°×\textbf{頂点の数}-360°)&=180°×\textbf{頂点の数}\end{align*}$$

したがって、外角の和は

$$\begin{align*}\textbf{外角の和}&=180°×\textbf{頂点の数}-(180°×\textbf{頂点の数}-360°)\\[0.5em]&=360°\end{align*}$$

となり、頂点の数によらず$\mathbf{360°}$で変わらないことがわかります。

　また、1つの内角に対し2つある外角をすべて足し合わせた場合は、倍の$\mathbf{720°}$となります。