三角形の重心は中線を何：何に内分する？

　「正三角形の重心が中線を2:1に内分するのはなんでだっけ……？」では正三角形だけにしか言及しませんでしたが、あらゆる三角形で重心がどんな性質を持っているかを調べてみます。

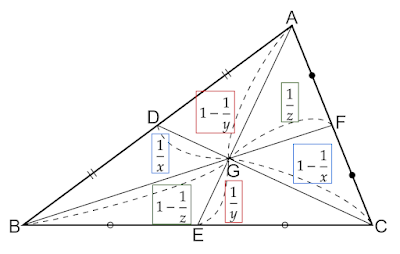
図1　三角形の重心

　正三角形の重心は中線を$1:2$に内分しましたが、他の三角形の場合で中線をすべて異なる比で内分する可能性を考慮して、図1のように重心$\text{G}$によって

\begin{align*}\text{GD}&=\frac{1}{x}\text{CD}\\[1em]\text{GE}&=\frac{1}{y}\text{AE}\\[1em]\text{GF}&=\frac{1}{z}\text{BF}\end{align*}

のように中線が分けられるとします。

図2　$△\text{ABC}$と$△\text{GAB}$の関係

　$△\text{GAB}$に着目すると、$\text{CD}:\text{GD}=1:\frac{1}{x}$は高さの比と等しくなる（※）ので、面積は

\begin{equation}△\text{GAB}=\frac{1}{x}△\text{ABC}\end{equation}

となります。

※三角形の一部分の面積を求めるの高さの関係参照

同様に$△\text{GBC, }△\text{GCA}$の面積も

\begin{align}△\text{GBC}&=\frac{1}{y}△\text{ABC}\\[1em]△\text{GCA}&=\frac{1}{z}△\text{ABC}\end{align}

となります。

図3　$△\text{ABF}$と$△\text{ABE}$

　次に、$△\text{ABF}$と$△\text{ABE}$に着目すると、$△\text{GAB}$の部分が共通しています。

したがって、

\begin{align*}△\text{ABF}&=△\text{GAB}+△\text{GFA}\\[1em]△\text{ABE}&=△\text{GAB}+△\text{GBE}\end{align*}

ここで、点$\text{E}$は$\text{BC}$の中点、点$\text{F}$は$\text{CA}$の中点なので

\begin{align}\begin{cases}△\text{ABF}&=\dfrac{1}{2}△\text{ABC}\\[0.5em]△\text{ABE}&=\dfrac{1}{2}△\text{ABC}\end{cases}\\[1em]\begin{cases}△\text{GFA}&=\dfrac{1}{2}△\text{GCA}\\[0.5em]△\text{GBE}&=\dfrac{1}{2}△\text{GBC}\end{cases}\end{align}

$(4)$より$△\text{ABF}$と$△\text{ABE}$の面積は等しいため、共通する$△\text{GAB}$の除いた$△\text{GFA}$と$△\text{GBE}$の面積も等しいとわかります。

$(2), (3), (5)$より、

\begin{align*}△\text{GFA}&=△\text{GBE}\\[0.5em]\frac{1}{2}△\text{GCA}&=\frac{1}{2}△\text{GBC}\\[0.5em]△\text{GCA}&=△\text{GBC}\\[0.5em]\frac{1}{z}△\text{ABC}&=\frac{1}{y}△\text{ABC}\\ \therefore y&=z\end{align*}

となり、中線$\text{AE}$と$\text{BF}$は重心$\text{G}$によって同じ比で内分されることがわかります。

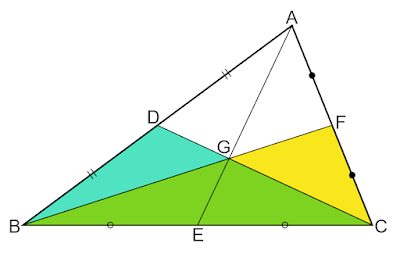
図4　$△\text{DBC}$と$△\text{FBC}$

　同様にして、$△\text{DBC}$と$△\text{FBC}$に着目すると、点$\text{D}$は$\text{AB}$の中点であることから$△\text{DBC}$と$△\text{FBC}$の面積は等しく、共通する$△\text{GBC}$を除いた$△\text{GDB}$と$△\text{GCF}$の面積も等しいことがわかります。

$△\text{GDB}$と$△\text{GCF}$はそれぞれ$△\text{GAB, }△\text{GCA}$の面積を2等分したものなので、$(1), (3)$より

\begin{align*}△\text{GDB}&=△\text{GCF}\\[0.5em]\frac{1}{2}△\text{GAB}&=\frac{1}{2}△\text{GCA}\\[0.5em]△\text{GAB}&=△\text{GCA}\\[0.5em]\frac{1}{x}△\text{ABC}&=\frac{1}{z}△\text{ABC}\\[0.5em]\therefore z&=x\end{align*}

となり、中線$\text{BF}$と$\text{CD}$は重心$\text{G}$によって同じ比で内分されることがわかります。

以上から、中線$\text{AE, BF, CD}$は重心$\text{G}$によってすべて同じ比で内分されることになります。
すなわち、$x=y=z$です。

$(1), (2), (3)$より、

\begin{align*}△\text{ABC}&=△\text{GAB}+△\text{GBC}+△\text{GCA}\\[0.5em]&=\frac{1}{x}△\text{ABC}+\frac{1}{x}△\text{ABC}+\frac{1}{x}△\text{ABC}\\[0.5em]&=\frac{3}{x}△\text{ABC}\\[0.5em]\therefore x&=3\end{align*}

となり、

\begin{align*}\text{CG}:\text{GD}&=1-\frac{1}{x}:\frac{1}{x}\\[0.5em]&=1-\frac{1}{3}:\frac{1}{3}\\[0.5em]&=\frac{2}{3}:\frac{1}{3}\\[0.5em]&=2:1\end{align*}

であるため、重心$\text{G}$は三角形の中線を$2:1$に内分することがわかりました。

　三角形の重心の性質は、上記の証明で明らかになったものを挙げると

1. 重心は中線を$2:1$に内分する。
2. 頂点と重心を線で結んだときにできる3つの三角形の面積は等しい。

があります。

2. に関連して3本の中線によって三角形の面積は6等分されるというものもあります。

関連：正三角形の重心が中線を2:1に内分するのはなんでだっけ……？