正六角形がおさまっている正方形の1辺の長さは？

図1　正方形に内接する正六角形

「図1のように正方形とその中に収まる正六角形がある。正六角形の1辺の長さが1のとき、正方形の1辺の長さはいくつになるか？」

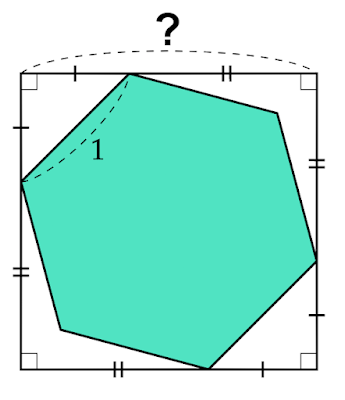
図2　正六角形の様々な長さ

　正六角形のいくつかの長さを調べます。
1辺の長さを$1$とすると、正六角形は合同な6つの正三角形に分割できることから、最も遠い頂点同士の距離は$2$、対辺同士の距離は$\sqrt{3}$となります。（鋭角の1つが$60°$の直角三角形の三角比より）

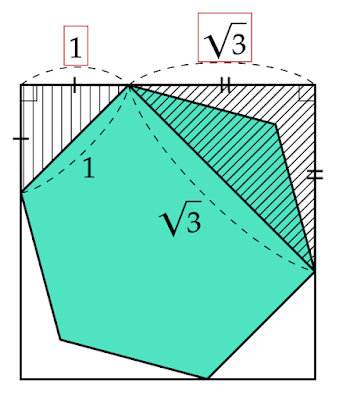
図3　2つの直角二等辺三角形

これを踏まえて図3のように補助線を引くと2つの直角二等辺三角形ができます。
それぞれの斜辺の長さは先ほどの六角形の長さより$1$と$\sqrt{3}$なので相似比は$1:\sqrt{3}$となります。

斜辺が$1$の直角二等辺三角形について考えると、等辺の長さを$a$として三平方の定理より

$$\begin{align*}a^2+a^2&=1^2\\ 2a^2&=1\\[0.5em]a^2&=\frac{1}{2}\\[0.5em]a&=\frac{\sqrt{2}}{2}&(\because a>0)\end{align*}$$

斜辺が$\sqrt{3}$の直角二等辺三角形の等辺の長さを$b$とすると相似比より

$$\begin{align*}1:\sqrt{3}&=\frac{\sqrt{2}}{2}:b\\[0.5em]b&=\sqrt{3}\cdot\frac{\sqrt{2}}{2}\\[0.5em]&=\frac{\sqrt{6}}{2}\end{align*}$$

正方形の1辺の長さは$a+b$となるので、

$$\begin{align*}a+b&=\frac{\sqrt{2}}{2}+\frac{\sqrt{6}}{2}\\[0.5em]&=\underline{\frac{\sqrt{2}+\sqrt{6}}{2}}≒1.93\end{align*}$$

と求められます。

　逆に正方形の1辺の長さを$1$とすると、正六角形の1辺の長さは

$$\begin{align*}\frac{2}{\sqrt{2}+\sqrt{6}}&=\frac{2}{\sqrt{2}(1+\sqrt{3})}\cdot\frac{\sqrt{2}(\sqrt{3}-1)}{\sqrt{2}(\sqrt{3}-1)}\\[0.5em]&=\frac{2\sqrt{2}(\sqrt{3}-1)}{4}\\[0.5em]&=\frac{\sqrt{2}(\sqrt{3}-1)}{2}\\[0.5em]&=\frac{\sqrt{6}-\sqrt{2}}{2}≒0.52\end{align*}$$

となります。