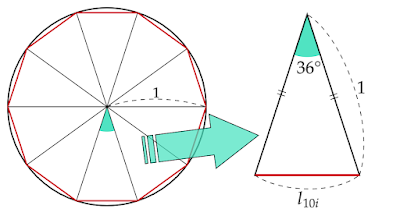
円に内接する正十角形
|
| 図1 円に内接する正十角形 |
半径1の円に内接する正十角形を考えます。円周の長さは$2\pi$となります。
円の中心を通る正十角形の対角線を引くと、10個の合同な二等辺三角形に分かれます。
頂角の大きさは$36°$で、等辺の長さは$1$です。
正十角形の周の長さを$L_{10i}$、正十角形の1辺でもある二等辺三角形の底辺の長さを$l_{10i}$とします。
すると、底辺の長さは余弦定理より
\begin{align*}{l_{10i}}^2&=1^2+1^2-2\cdot1\cdot1\cos36°\\
&=2-2\cos36°\end{align*}
ここで、以前の記事より$\cos36°$は
\[\cos36°=\frac{1+\sqrt{5}}{4}\]
となることがわかったので、
\begin{align*}{l_{10i}}^2&=2-2\cdot\frac{1+\sqrt{5}}{4}\\
&=\frac{3-\sqrt{5}}{2}\\ l_{10i}&=\sqrt{\frac{3-\sqrt{5}}{2}}\\
&=\sqrt{\frac{6-2\sqrt{5}}{4}}\\
&=\sqrt{\frac{(\sqrt{5}-1)^2}{4}}\\
&=\frac{\sqrt{5}-1}{2}\end{align*}
となります。
\[L_{10i}=10l_{10i}\]
なので、正十角形の周の長さは
\begin{align*}L_{10i}&=10\cdot\frac{\sqrt{5}-1}{2}\\
&=5\sqrt{5}-5&≒\underline{6.18}\end{align*}
となります。
したがって、円に内接する正十角形の周の長さと円周の関係は、
\begin{align*}2\pi:5\sqrt{5}-5&=\pi:\frac{5\sqrt{5}-5}{2}\\
&≒\pi:3.09\end{align*}
円に内接する正十角形の周の長さは円周より短いので$\pi>3.09$であるとわかります。
円に外接する正十角形
|
| 図2 円に外接する正十角形 |
半径1の円に外接する正十角形を考えます。円周は先ほどと同じ$2\pi$です。
円の中心を通る正十角形の対角線を引くと10個の合同な二等辺三角形に分かれます。
頂角の大きさは$36°$、高さは$1$です。
正十角形の周の長さを$L_{10o}$、二等辺三角形の底辺の長さは$l_{10o}$とします。
頂角と底辺の中点を通る直線で二等辺三角形を分割したときできる直角三角形について考えると、
\begin{align*}\frac{l_{10o}}{2}&=1\cdot\tan(\frac{36°}{2})\\
l_{10o}&=2\tan(\frac{36°}{2})\end{align*}
ここで、半角の公式の
\[\tan^2\frac{\theta}{2}=\frac{1-\cos\theta}{1+\cos\theta}\]
から
\[\tan\frac{\theta}{2}=\frac{\sin\theta}{1+\cos\theta}\qquad(0°<\theta<90°)\]
が得られるので、
\[l_{10o}=\frac{2\sin36°}{1+\cos36°}\]
$sin36°$は以前の記事より、
\[sin36°=\sqrt{\frac{5-\sqrt{5}}{8}}\]
なので、
\begin{align*}l_{10o}&=\frac{2\sqrt{\frac{5-\sqrt{5}}{8}}}{1+\frac{1+\sqrt{5}}{4}}\\
&=\frac{\sqrt{\frac{5-\sqrt{5}}{2}}}{\frac{5+\sqrt{5}}{4}}\\
&=\frac{4}{\sqrt{2}}\cdot\frac{\sqrt{5-\sqrt{5}}}{5+\sqrt{5}}\\
&=2\sqrt{2}\cdot\frac{\sqrt{5-\sqrt{5}}}{5+\sqrt{5}}\cdot\frac{5-\sqrt{5}}{5-\sqrt{5}}\\
&=\frac{2\sqrt{2}(5-\sqrt{5})\sqrt{5-\sqrt{5}}}{20}\\
&=\frac{\sqrt{2}(5-\sqrt{5})\sqrt{5-\sqrt{5}}}{10}\end{align*}
となります。
\[L_{10i}=10l_{10i}\]
なので、正十角形の周の長さは
\begin{align*}L_{10o}&=10\cdot\frac{\sqrt{2}(5-\sqrt{5})\sqrt{5-\sqrt{5}}}{10}\\
&=\sqrt{2}(5-\sqrt{5})\sqrt{5-\sqrt{5}}&≒\underline{6.50}\end{align*}
となります。
したがって、円に外接する正十角形と円周の関係は
\begin{align*}2\pi:\sqrt{2}(5-\sqrt{5})\sqrt{5-\sqrt{5}}&=\pi:\frac{\sqrt{2}(5-\sqrt{5})\sqrt{5-\sqrt{5}}}{2}\\
&≒\pi:3.25\end{align*}
円に外接する正十角形の周の長さは円周より長いので、$\pi<3.25$であることがわかります。
以上のことから、円に内接・外接する正十角形の周の長さから円周率$\pi$の値を絞り込んでみると$3.09<\pi<3.25$の範囲内にあることがわかりました。
Share:
