必要条件、十分条件 どっち？

　命題には、必要条件と十分条件というものがあり、

「AならばB」が真であるとき、

BはAであるための必要条件

AはBであるための十分条件

と説明されます。この部分をもう少し掘り下げてみたいと思います。

必要条件と十分条件 どっちがどっち？

　命題の例として「正方形ならば4辺が等しい」を挙げます。正方形の4辺は等しいので、この命題は真です。
この命題の場合、「正方形（である）」が十分条件、「4辺が等しい」が必要条件となりますが、この2つの条件についてもう少し考えてみます。

図1　4辺がすべて等しい四角形

　四角形の分類を考えると、「4辺が等しい」に当てはまるのはひし形とひし形の一種の正方形です。

十分条件：

このことから正方形は「4辺が等しい」という条件を”十分に”満たした四角形だといえます。すなわち、「正方形（である）」は「4辺が等しい」を満たす十分（な）条件ということになります。

必要条件：

また、逆に「正方形」の特徴を表すもので「4辺が等しい」というのは外すことのできない”必要な”ものであるとも言えます。すなわち、「4辺が等しい」は「正方形」であるための必要（な）条件となるのです。

以上から、命題が成立するためには図1のように必要条件の中に十分条件がすっぽり入っていることが求められます。

　次に、命題の逆を考えると「4辺が等しいならば正方形である」となります。図1より、4辺がすべて等しい四角形にはひし形も含まれるため正方形であるとは言い切れません。したがって、この命題の逆は偽となります。
2つの条件「4辺が等しい」と「正方形である」について考えます。

「4辺が等しい」は「正方形である」という条件を十分に満たしているか、つまり正方形だけで「4辺が等しい」四角形を表すことができるかというとできません。
前述の通りひし形も「4辺が等しい」四角形だからです。なので、十分条件になっていません。

また、「正方形である」は「4辺が等しい」四角形を表す条件として必須であるかというとこれも違います。

図2　正方形の条件

正方形の特徴について考えると、「4辺が等しい」以外に「内角がすべて直角である」があります。しかし、同じく「4辺が等しい」という条件があるひし形は内角は直角である必要はありません。
すなわち、「正方形である」ことの条件の内、「内角がすべて直角である」が余計なのでこれを必要条件とするには不適切になります。

　以上のことから必要条件と十分条件について以下のようなことがわかります。

• 命題が真でないと必要条件も十分条件もない。
• 「ならば」の前が十分条件となる。条件の範囲は必要条件より狭い。
• 「ならば」の後が必要条件となる。条件の範囲は十分条件を内包している。

必要十分条件とは？

　命題の条件には必要十分条件というものがあります。これは

命題「AならばB」と逆「BならばA」が真であるとき、

AはBであるための、BはAであるための必要十分条件

と説明されます。

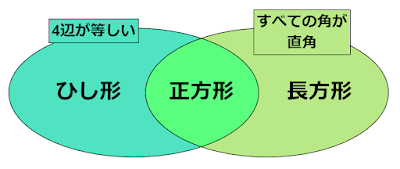
　例えば、「4辺が等しく、内角がすべて直角ならば正方形である」という命題を考えます。

図3　正方形の条件

「4辺が等しく、内角が全て直角」な四角形は正方形しかありません。なので、この命題は真です。
また、命題の逆「正方形ならば4辺が等しく、内角がすべて直角である」も真となります。
このことから、「4辺が等しく、内角がすべて直角」と「正方形である」はともに十分条件と必要条件の両方になることができます。なので、2つの条件は必要十分条件となります。

必要十分条件のとき図3のように十分条件と必要条件の範囲は全く同じとなります。