重心の位置ベクトルの求め方 2通り

　重心の位置ベクトルは以下のようになります。

図1　重心の位置ベクトル

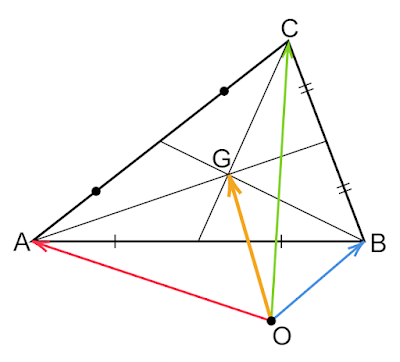
　$△\text{ABC}$の重心$\text{G}$の位置ベクトル$\vec{\text{OG}}$は

$$\vec{\text{OG}}=\frac{\vec{\text{OA}}+\vec{\text{OB}}+\vec{\text{OC}}}{3}$$

これを2通りの方法で求めてみました。

その1

図2　重心の位置ベクトルを求める

　重心の位置ベクトル$\vec{\text{OG}}$を$\vec{\text{OA}}$と$\vec{\text{AG}}$の2つのベクトルの合成で求めます。
そのために$△\text{ABC}$と合同な三角形を組み合わせた平行四辺形$\text{ABA'C}$を考え、$\vec{\text{AG}}$を$\vec{\text{OA}},\vec{\text{OB}},\vec{\text{OC}}$で表します。

$$\vec{\text{AA'}}=\vec{\text{AB}}+\vec{\text{BA'}}$$

となるため、

$$\begin{align*}\vec{\text{AB}}&=\vec{\text{OB}}-\vec{\text{OA}}\\[1em]\vec{\text{BA'}}&=\vec{\text{AC}}\\[0.5em]&=\vec{\text{OC}}-\vec{\text{OA}}\\[1em]\vec{\text{AA'}}&=\vec{\text{OB}}-\vec{\text{OA}}+\vec{\text{OC}}-\vec{\text{OA}}\\[0.5em]&=\vec{\text{OB}}+\vec{\text{OC}}-2\vec{\text{OA}}\end{align*}$$

$\text{BC}$の中点を$\text{D}$とすると、重心$\text{G}$は中線$\text{AD}$を$2:1$に内分することと$\text{AD}=\text{DA'}$から、

$$\begin{align*}\text{AG}:\text{GD}:\text{DA'}&=2:1:3\\[1em]\text{AG}:\text{AA'}&=\text{AG}:\text{AG}+\text{GD}+\text{DA'}\\[0.5em]&=2:2+1+3=1:3\end{align*}$$

このことから、

$$\begin{align*}\vec{\text{AG}}&=\frac{1}{3}\vec{\text{AA'}}\\[0.5em]&=\frac{\vec{\text{OB}}+\vec{\text{OC}}-2\vec{\text{OA}}}{3}\end{align*}$$

よって、

$$\begin{align*}\vec{\text{OG}}&=\vec{\text{OA}}+\vec{\text{AG}}\\[0.5em]&=\vec{\text{OA}}+\frac{\vec{\text{OB}}+\vec{\text{OC}}-2\vec{\text{OA}}}{3}\\[0.5em]&=\frac{\vec{\text{OA}}+\vec{\text{OB}}+\vec{\text{OC}}}{3}\end{align*}$$

その2

　重心の位置ベクトル$\vec{\text{OG}}$を$\vec{\text{OA}},\vec{\text{AE}},\vec{\text{EG}}$の合成で求めます。ただし、点$\text{E}$は$\text{AC}$の中点です。
そのために$\vec{\text{AE}},\vec{\text{EG}}$を$\vec{\text{OA}},\vec{\text{OB}},\vec{\text{OC}}$で表します。

$$\begin{align*}\vec{\text{AE}}&=\frac{1}{2}\vec{\text{AC}}\\[0.5em]&=\frac{\vec{\text{OC}}-\vec{\text{OA}}}{2}\end{align*}$$

点$\text{G}$は$△\text{ABC}$の重心であるから、

$$\text{BG}:\text{GE}=2:1$$

このことから$\vec{\text{EG}}$は

$$\begin{align*}\vec{\text{EG}}&=\frac{1}{3}\vec{\text{EB}}\\[0.5em]&=\frac{\vec{\text{OB}}-\vec{\text{OE}}}{3}\end{align*}$$

ここで、$\vec{\text{OE}}$は

$$\begin{align*}\vec{\text{OE}}&=\vec{\text{OA}}+\vec{\text{AE}}\\[0.5em]&=\vec{\text{OA}}+\frac{\vec{\text{OC}}-\vec{\text{OA}}}{2}\\[0.5em]&=\frac{\vec{\text{OA}}+\vec{\text{OC}}}{2}\end{align*}$$

したがって、

$$\begin{align*}\vec{\text{EG}}&=\frac{1}{3}\left(\vec{\text{OB}}-\frac{\vec{\text{OA}}+\vec{\text{OC}}}{2}\right)\\[0.5em]&=\frac{2\vec{\text{OB}}-\vec{\text{OA}}-\vec{\text{OC}}}{6}\end{align*}$$

よって、$\vec{\text{OG}}$は

$$\begin{align*}\vec{\text{OG}}&=\vec{\text{OA}}+\vec{\text{AE}}+\vec{\text{EG}}\\[0.5em]&=\vec{\text{OA}}+\frac{\vec{\text{OC}}-\vec{\text{OA}}}{2}+\frac{2\vec{\text{OB}}-\vec{\text{OA}}-\vec{\text{OC}}}{6}\\[0.5em]&=\frac{\vec{\text{OA}}+\vec{\text{OB}}+\vec{\text{OC}}}{3}\end{align*}$$