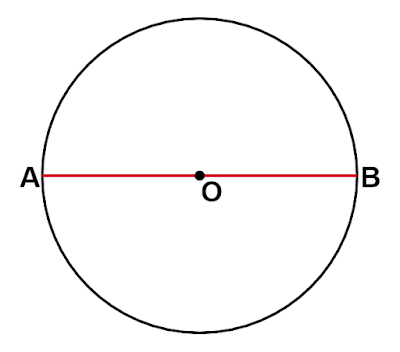
正五角形は以下のように定規とコンパスを使って作図します。
正五角形の作図法
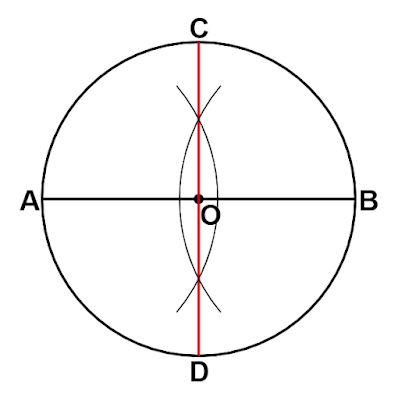
1.
2.
3.
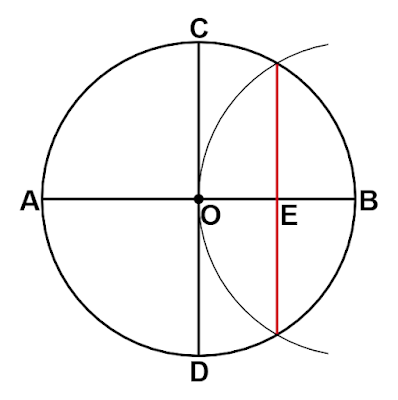
4.
5.
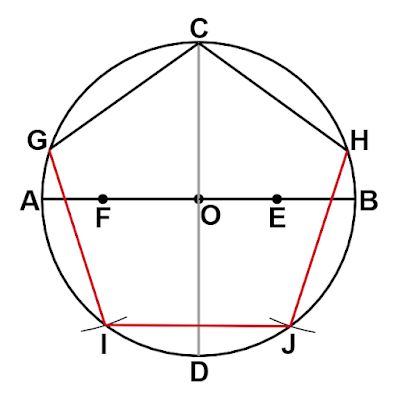
線分$\text{CG, CH}$を引くとこれらが正五角形の辺となります。
6.
7.
本当に正五角形か？
本当に正五角形であるのかを手順4.、5.で作図に使用している長さを調べてみます。
円$\text{O}$の半径を$1$とすると、$\text{OC}=1$です。点$\text{E}$は$\text{OB}$の中点なので$\text{OE}=\dfrac{1}{2}$となります。三平方の定理より
\begin{align*}\text{CE}^2&=\text{OC}^2+\text{OE}^2\\[0.5em]&=1^2+\left(\frac{1}{2}\right)^2\\[0.5em]&=\frac{5}{4}\\[0.5em]\therefore
\text{CE}&=\frac{\sqrt{5}}{2}&(\because \text{CE}>0)\end{align*}
となります。
前述の通り$\text{OC}=1$です。図形$\text{CFE}$はおうぎ形で$\text{CE}=\text{FE}=\dfrac{\sqrt{5}}{2}$です。
また、$\text{OE}=\dfrac{1}{2}$なので
\begin{align*}\text{OF}&=\text{FE-OE}\\[0.5em]&=\frac{\sqrt{5}-1}{2}\end{align*}
となります。さらに、三平方の定理より
\begin{align*}\text{CF}^2&=\text{OC}^2+\text{OE}^2\\[0.5em]&=1^2+\left(\frac{\sqrt{5}-1}{2}\right)^2\\[0.5em]&=1-\frac{6-2\sqrt{5}}{4}\\[0.5em]&=\frac{10-2\sqrt{5}}{4}\\[0.5em]\therefore
\text{CF}&=\frac{\sqrt{10-2\sqrt{5}}}{2}&(\because \text{CF}>0)\end{align*}
となります。
$\text{CF}$の長さを元に正五角形の辺となる線分を引くことになるので、これが正五角形の1辺の長さとなります。
円に内接・外接する正五角形の周の長さと円周率の関係で求めた半径$1$の円に内接する正五角形の1辺の長さも$\dfrac{\sqrt{10-2\sqrt{5}}}{2}$なので、作図されたのは確かに正五角形であることがわかります。
参考：鈴木進吾 他（編）、2003、「学研版 算数おもしろ大事典」、株式会社学習研究社
Share:
