正三角形の作図法

　正三角形の定規とコンパスを使った作図法を2通り紹介します。

その1

1.

線分$\text{AB}$を引き、$\text{AB}$と同じ長さの円弧を両端をそれぞれ中心として描きます。
そして、2つの円弧の交点を$\text{C}$とします。

2.

線分$\text{AC,} \text{BC}$を引きます。

3.

正三角形$\text{ABC}$を作図できました。

　この方法は線分の長さを元にして円の半径の性質、円の中心と円周の距離（＝半径）はどの部分でも同じであることを利用した作図法です。

その2

1.

円を描き、直径$\text{AB}$を引きます。

2.

直径の1端から円の半径と同じ円弧を描き、円周との交点を利用して線分$\text{CD}$を作図します。

3.

線分$\text{AC,} \text{AD}$を引きます。

4.

正三角形$\text{ACD}$が作図できました。

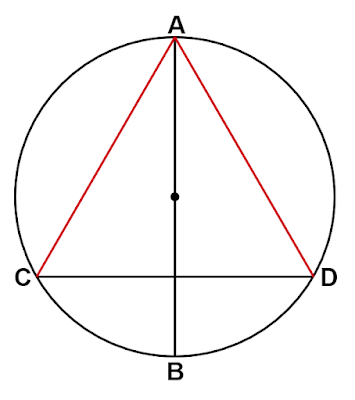
　こちらは線分の長さではなく、2つの円が交わったときの性質と円周角の性質を利用して正三角形を作図しています。

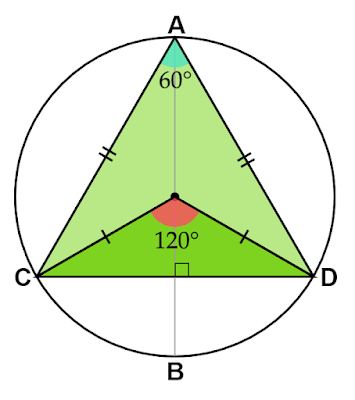
点$\text{C,} \text{D}$を通る半径によってできる中心角は$120°$になります。$\text{AC,} \text{AD}$によってできる円周角は中心角の半分の$60°$となります。

また$\text{AC}=\text{AD}$なので、$△\text{ACD}$は頂角が$60°$の二等辺三角形＝正三角形であることがわかります。

関連：同じ半径の2円の中心が互いの円周上にあるときにできる扇形の中心角は？

関連：頂角が60°の二等辺三角形が正三角形であることの証明