角の二等分線の作図法

　角の二等分線は以下のように定規とコンパスを使って作図します。

1.

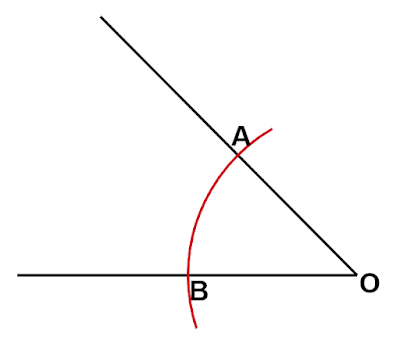
頂点$\text{O}$を中心とする円弧を描きます。円弧は角をつくる2直線に交わるように描きます。

2.

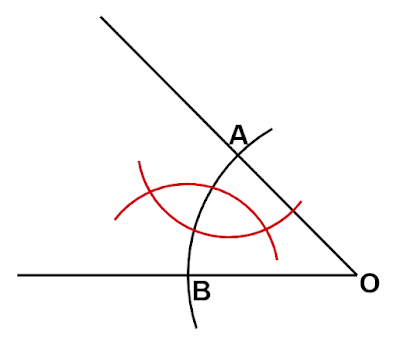
円弧と2直線との交点$\text{A, B}$からそれぞれ半径が同じ円弧を描きます。
ここで描いた円弧同士の交点は2つである必要はなく、1つだけでも大丈夫です。

3.

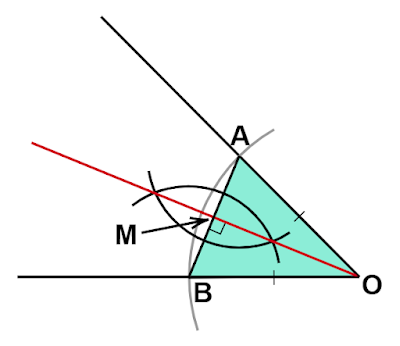
頂点$\text{O}$と2. でできた交点を通る直線を引きます。
この直線が$∠\text{AOB}$の二等分線となります。

　なぜこれで角の二等分線を作図できるのかを考えます。

$△\text{OAB}$を考えるとこの三角形は$\text{OA}=\text{OB}$となる二等辺三角形となります。

この三角形において2. 以降でおこなう作業は底辺$\text{AB}$の垂直二等分線の作図となります。
底辺の垂直二等分線$\text{OM}$は二等辺三角形を2つの合同な直角三角形に分割するので頂角である$∠\text{AOB}$も2等分されます。

したがって、$\text{AB}$の垂直二等分線は$∠\text{AOB}$の二等分線でもあることがわかります。

関連：二等辺三角形の特徴

関連：垂直二等分線の作図