長方形の各頂点と任意の点を結ぶ線分の長さの関係

　長方形の各頂点と任意の点を結ぶ4本の線分の長さにはどのような関係があるでしょうか？

　長方形$ABCD$と任意の点$P$を考え、点$P$の位置を3つの場合に分けて考えます。

点$P$が長方形の内部にある場合

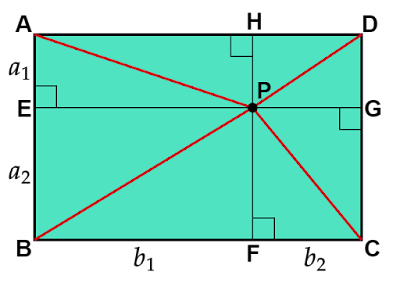
　点$P$から長方形の各辺へ垂線をおろし、辺$AB,BC,CD,DA$との交点をそれぞれ$E,F,G,H$とします。
このとき四角形$AEPH,BEPF,CFPG,DGPH$は長方形であり、$AE=a_1,BE=a_2,$$BF=b_1,CF=b_2$とおくと長方形の対辺の長さは等しいので$HP=a_1,CG=FP=a_2,$$EP=b_1,DH=GP=b_2$となることがわかります。

線分$AP$は長方形$AEPH$の対角線であり$△AEP$は直角三角形なので三平方の定理より

$$\begin{align*}AP^2&=AE^2+EP^2\\[0.5em]&={a_1}^2+{b_1}^2\tag1\end{align*}$$

線分$BP$は長方形$BEPF$の対角線であり$△BFP$は直角三角形なので

$$\begin{align*}BP^2&=FP^2+BF^2\\[0.5em]&={a_2}^2+{b_1}^2\tag2\end{align*}$$

線分$CP$は長方形$CFPG$の対角線であり$△CGP$は直角三角形なので

$$\begin{align*}CP^2&=CG^2+GP^2\\[0.5em]&={a_2}^2+{b_2}^2\tag3\end{align*}$$

線分$DP$は長方形$DGPH$の対角線であり$△DHP$は直角三角形なので

$$\begin{align*}DP^2&=HP^2+DH^2\\[0.5em]&={a_1}^2+{b_2}^2\tag4\end{align*}$$

となります。

$(1)+(3)$より

$$AP^2+CP^2={a_1}^2+{a_2}^2+{b_1}^2+{b_2}^2$$

$(2)+(4)$より

$$BP^2+DP^2={a_1}^2+{a_2}^2+{b_1}^2+{b_2}^2$$

なので

$$\large AP^2+CP^2=BP^2+DP^2$$

が成り立つことがわかります。

点$P$が長方形の周上にある場合

　点$P$が長方形$ABCD$の周上にある場合はさらに2つの場合に分けることができます。

点$P$が頂点を除く辺上にある場合

　点$A,B$とは異なる辺$AB$上に点$P$がある場合を考えます。
$BC=b$とおくと長方形の対辺の長さは等しいので$DA=b$となります。
点$P$から対辺$CD$へ垂線をおろし、その足を$Q$とすると長方形$ABCD$は長方形$ADQP$と長方形$BCQP$ができます。

長方形$ADQP$において線分$AP$は辺の1つ、線分$DP$は対角線であり$△ADP$は直角三角形なので三平方の定理より

$$\begin{align*}DP^2&=AP^2+DA^2\\[0.5em]&=AP^2+b^2\\[0.5em]\therefore b^2&=DP^2-AP^2\tag5\end{align*}$$

長方形$BCQP$において線分$BP$は辺の1つ、線分$CP$は対角線であり$△BCP$は直角三角形なので

$$\begin{align*}CP^2&=BP^2+BC^2\\[0.5em]&=BP^2+b^2\\[0.5em]\therefore b^2&=CP^2-BP^2\tag6\end{align*}$$

となります。

$(5),(6)$より

$$\begin{align*}DP^2-AP^2&=CP^2-BP^2\\[0.5em]\therefore\large AP^2+CP^2&\large=BP^2+DP^2\end{align*}$$

が成り立つことがわかります。

点$P$が他の辺上にある場合も同様です。

点$P$が頂点と重なる場合

　点$P$が頂点$A$と重なる場合を考えます。
このとき$AP=0$であり、線分$BP,DP$はそれぞれ辺$AB,DA$と、線分$CP$は長方形$ABCD$の対角線$AC$と重なるため$BP=AB,CP=AC,DP=DA$となります。
また、長方形の対辺の長さは等しいので$BC=DA$より$DP=BC$です。

$△ABC$は直角三角形なので三平方の定理より

$$\begin{align*}AC^2&=AB^2+BC^2\\[0.5em]\therefore\large CP^2&\large=BP^2+DP^2\end{align*}$$

が成り立つことがわかります。

これは$AP^2+CP^2=BP^2+DP^2$に$AP=0$を代入したときの式と一致するため、この場合においても$AP^2+CP^2=BP^2+DP^2$を満たしていることがわかります。
点$P$が他の頂点と重なる場合も同様です。

点$P$が長方形の外部にある場合

　点$P$が長方形の外部にある場合は大きく2つの場合に分けることができます。

点$P$がいずれかの辺の延長上にある場合

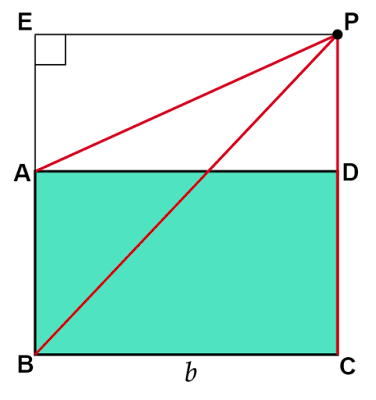
　上図のように点$P$が辺$CD$の延長上にある場合を考えます。
点$P$から辺$CD$以外の辺またはその延長に垂線をおろし、辺$AB$の延長との交点を$E$とします。なお、辺$BC$との交点は点$C$、辺$DA$との交点は点$D$です。
$BC=b$とおくと、長方形の対辺の長さは等しいので$DA=b$となります。
また、四角形$ADPE,BCPE$は長方形であることがわかります。

長方形$ADPE$において線分$DP$は辺の1つ、線分$AP$は対角線であり$△ADP$は直角三角形なので三平方の定理より

$$\begin{align*}AP^2&=DP^2+AD^2\\[0.5em]&=DP^2+b^2\\[0.5em]\therefore b^2&=AP^2-DP^2\tag7\end{align*}$$

長方形$BCPE$において線分$CP$は辺の1つ、線分$BP$は対角線であり$△BCP$は直角三角形なので

$$\begin{align*}BP^2&=CP^2+BC^2\\[0.5em]&=CP^2+b^2\\[0.5em]\therefore b^2&=BP^2-CP^2\tag8\end{align*}$$

となります。

$(7),(8)$より

$$\begin{align*}AP^2-DP^2&=BP^2-CP^2\\[0.5em]\therefore\large AP^2+CP^2&=BP^2+DP^2\end{align*}$$

が成り立つことがわかります。
点$P$が他の辺の延長上にある場合も同様です。

点$P$がどの辺の延長上にもない場合

　点$P$がどの辺の延長上にもない場合はさらに細かく2つの場合に分けることができます。

点$P$が1組の対辺へ直接垂線を下ろせる場合

　上図のように点$P$が長方形$ABCD$の外部かつ辺$BC,DA$に直接垂線を下ろせる位置にある場合を考えます。
点$P$から各辺またはその延長に垂線をおろし、辺$AB,CD$の延長との交点をそれぞれ$E,G$、辺$BC,DA$との交点を$F,H$をします。
辺$AB$の長さを$AB=a$、その延長部分$AE$の長さを$AE=a'$とおくと$BE=a+a'$となります。
また、四角形$AEPH,BEPF,CFPG,DHPG$は長方形であり、長方形の対辺の長さは等しいので$FP=a+a',HP=a',$$AH=b,DH=b'$となります。

線分$AP$は長方形$AEPH$の対角線で$△AHP$は直角三角形なので三平方の定理より

$$\begin{align*}AP^2&=HP^2+AH^2\\[0.5em]&={a'}^2+{b_1}^2\tag9\end{align*}$$

線分$BP$は長方形$BEPF$の対角線で$△BFP$は直角三角形なので

$$\begin{align*}BP^2&=FP^2+BF^2\\[0.5em]&=(a+a')^2+{b_1}^2\tag{10}\end{align*}$$

線分$CP$は長方形$CFPG$の対角線で$△CFP$は直角三角形なので

$$\begin{align*}CP^2&=FP^2+CF^2\\[0.5em]&=(a+a')^2+{b_2}^2\tag{11}\end{align*}$$

線分$DP$は長方形$DHPG$の対角線で$△DHP$は直角三角形なので

$$\begin{align*}DP^2&=HP^2+DH^2\\[0.5em]&={a'}^2+{b_2}^2\tag{12}\end{align*}$$

となります。

$(9)+(11)$より

$$AP^2+CP^2=(a+a')^2+{a'}^2+{b_1}^2+{b_2}^2$$

$(10)+(12)$より

$$BP^2+DP^2=(a+a')^2+{a'}^2+{b_1}^2+{b_2}^2$$

なので

$$\large AP^2+CP^2=BP^2+DP^2$$

が成り立ちます。
これは点$P$が長方形$ABCD$の外部かつ辺$AB,CD$に直接垂線を下ろせる位置にある場合も同様です。

点$P$がどの対辺の組へも直接垂線を下ろせない場合

　点$P$が上図の位置にある場合を考えます。
点$P$から長方形の各辺の延長へ垂線をおろし、辺$AB,BC,CD,DA$の延長との交点をそれぞれ$E,F,G,H$とします。
辺$AB,BC$とこれらの延長部分の長さについて$AB=a,BC=b,$$AE=a',CF=b'$とおくと$BE=a+a',BF=b+b'$となります。
また、四角形$AEPH,BEPF,CFPG,DGPH$は長方形であり、長方形の対辺の長さは等しいので$HP=a',FP=a+a',$$GP=b',EP=b+b'$となることがわかります。

線分$AP$は長方形$AEPH$の対角線であり$△AHP$は直角三角形なので三平方の定理より

$$\begin{align*}AP^2&=PH^2+AH^2\\[0.5em]&={a'}^2+(b+b')^2\tag{13}\end{align*}$$

線分$BP$は長方形$BEPF$の対角線であり$△BFP$は直角三角形なので

$$\begin{align*}BP^2&=FP^2+BF^2\\[0.5em]&=(a+a')^2+(b+b')^2\tag{14}\end{align*}$$

線分$CP$は長方形$CFPG$の対角線であり$△CFP$は直角三角形なので

$$\begin{align*}CP^2&=FP^2+CF^2\\[0.5em]&=(a+a')^2+{b'}^2\tag{15}\end{align*}$$

線分$DP$は長方形$DGPH$の対角線であり$△DHP$は直角三角形なので

$$\begin{align*}DP^2&=HP^2+DH^2\\[0.5em]&={a'}^2+{b'}^2\tag{16}\end{align*}$$

となります。

$(13)+(15)$より

$$AP^2+CP^2=(a+a')^2+{a'}^2+(b+b')^2+{b'}^2$$

$(14)+(16)$より

$$BP^2+DP^2=(a+a')^2+{a'}^2+(b+b')^2+{b'}^2$$

なので

$$\large AP^2+CP^2=BP^2+DP^2$$

が成り立つことがわかります。

これはこの場合を満たす他の位置に点$P$がある場合も同様です。

以上より、点$P$がどの位置にあっても長方形$ABCD$の各頂点と点$P$を結ぶ線分について

$$\large AP^2+CP^2=BP^2+DP^2$$

が成り立つことがわかります。

関連：三平方の定理（ピタゴラスの定理）