定積分の値が負の値になることがあるのはなぜなのか？

　定積分$\int_a^b{f(x)}dx$はなぜ負の値になることがあるのでしょうか？

　定積分$\int_a^b{f(x)}dx$は$y=f(x)$とx軸、直線$x=a,x=b$に囲まれた部分の面積を求める計算となります。

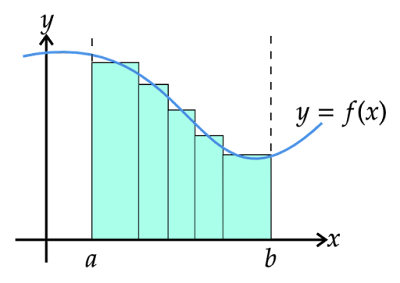
$y=f(x)$とx軸、直線$x=a,x=b$に囲まれた部分の面積はy軸に平行な直線を使って分割し、それぞれの部分を近似した長方形に置き換え、すべての長方形の面積を足し合わせることで求めます。これが定積分の根本にある考え方です。

　これら近似した長方形の辺の長さは符号を考慮した長さとなります。符号を考慮した長さとは、測りはじめの基準点と基準となる向きがあるため負の値にもなりうる長さのことです。

関連：符号を考慮した長さとは？

数直線において数直線の矢印の方向を正とすると、数直線上の測りはじめの基準点から数直線の矢印方向にある点までの距離は正の値、基準点から数直線の矢印と逆方向にある点までの距離は負の値で表すことになります。符号を考慮した長さは終端となる点の座標から基準点の座標を引いた値によって表されます。
また、数直線の座標も数直線の矢印の方向を正、$0$を基準点としたときの各点までの符号を考慮した距離と考えることができます。

定積分$\int_a^b{f(x)}dx$において、x軸に平行な線分の長さはx軸方向を正として下端$a$により近い端点を基準点として測ります。$a\leqq b$のときx軸方向と同方向に測ることになるので長さは正の値となります。逆に$a\geqq b$のときはx軸方向と逆方向に測ることになるので長さは負の値となります。

　$y=f(x)$とx軸、直線$x=a$、$x=b$に囲まれた部分のうち2つの直線$x=x_n,x=x_{n+1}$（ただし$x_n<x_{n+1}$）間の近似した長方形に着目して考えます。このとき長方形のy軸に平行な辺の長さは$x=p$（ただし$x_n\leqq p\leqq x_{n+1}$）における$f(x)$の値$f(p)$とします。

$a\leqq b$かつ$f(p)\geqq0$のとき

長方形のx軸に平行な辺の長さは$a\leqq b$より$0$以上の値なので$x_{n+1}-x_n$、y軸に平行な辺の長さは$f(p)\geqq0$です。したがって、この2辺の長さの積より求められる長方形の面積は2つの正の数の積なので$(x_{n+1}-x_n)f(p)\geqq0$となります。

このことから$a\leqq x\leqq b$において常に$f(x)\geqq0$のとき$\int_a^b{f(x)}dx\geqq0$となります。

$a\leqq b$かつ$f(p)\leqq0$のとき

長方形のx軸に平行な辺の長さは$a\leqq b$より$x_{n+1}-x_n$、y軸に平行な辺の長さは$f(p)\leqq0$です。

したがって、長方形の面積は正の数と負の数の積なので$(x_{n+1}-x_n)f(p)\leqq0$となります。

このことから$a\leqq x\leqq b$において常に$f(x)\leqq0$のとき$\int_a^b{f(x)}dx\leqq0$となります。

$a\geqq b$かつ$f(p)\geqq0$のとき

長方形のx軸に平行な辺の長さは$a\leqq b$より$0$以下の値なので$x_n-x_{n+1}$、y軸に平行な辺の長さは$f(p)\geqq0$です。

したがって、長方形の面積は負の数と正の数の積なので$(x_n-x_{n+1})f(p)\leqq0$となります。

このことから$b\leqq x\leqq a$において常に$f(x)\geqq0$のとき$\int_a^b{f(x)}dx\leqq0$となります。

$a\geqq b$かつ$f(p)\leqq0$のとき

長方形のx軸に平行な辺の長さは$a\leqq b$より$x_n-x_{n+1}$、y軸に平行な辺の長さは$f(p)\leqq0$です。

したがって、長方形の面積は2つの負の数の積なので$(x_n-x_{n+1})f(p)\geqq0$となります。

このことから$b\leqq x\leqq a$において常に$f(x)\leqq0$のとき$\int_a^b{f(x)}dx\geqq0$となります。

以上のように符号を考慮した長さをもちいた結果、求める面積も符号を考慮したものとなるため定積分には負の値が存在します。

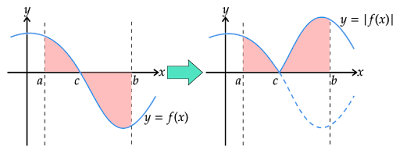
　積分区間$a\leqq x\leqq b$で$f(x)$の正負が入れ替わる、例えば上図のように$a\leqq x\leqq c$で$f(x)\geqq0$、$c\leqq x\leqq b$で$f(x)\leqq0$となる場合を考えます。

$y=f(x)$とx軸と直線$x=a$で囲まれた部分の面積を$S_1$、$y=f(x)$とx軸と直線$x=b$で囲まれた部分の面積を$S_2$とすると定積分$\int_a^b{f(x)}dx$の値はこれらの面積の和となるので$S_1+S_2$なのですが、定積分では$S_1$は正の値、$S_2$は負の値となるので絶対値をもちいて表せば

\begin{align*}\int_a^b{f(x)}dx&=S_1+S_2\\[0.5em]&=|S_1|+\bigl(-|S_2|\bigr)\\[0.5em]&=|S_1|-|S_2|\end{align*}

となります。

$S_1,S_2$がともに符号を考慮しない面積であればどちらも正の値で

\[S_1+S_2=|S_1|+|S_2|\]

となるはずなので定積分における面積の和は符号を考慮しない面積の和とは異なる結果になります。

定積分を利用して$y=f(x)$とx軸、直線$x=a,x=b$に囲まれた部分の符号を考慮しない面積を求めるには$a,b$を$a<b$となるように定め、$y=f(x)$を$y=|f(x)|$に置き換えて$\int_a^b|f(x)|dx$を計算する必要があります。