へこんでいる部分のある四角形の内角の和は何度？

図1　凹四角形

　四角形の内角の和は$360°$です。では、へこんでいる部分のある四角形（凹四角形）の内角の和も$360°$になるのでしょうか？

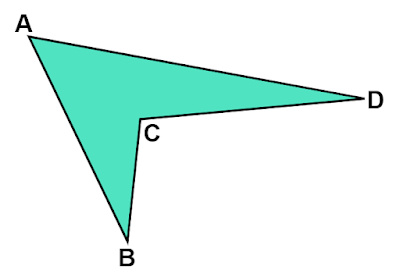
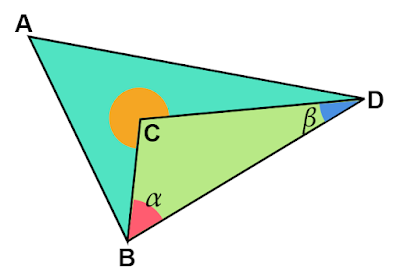
図2　凹四角形の内角の和の導出

　図2のように凹四角形$\text{ABCD}$の凹部の頂点$\text{C}$に隣接する頂点$\text{B, D}$を線で結ぶと大きい三角形$\text{ABD}$と小さい三角形$\text{CBD}$ができます。
凹四角形$\text{ABCD}$の内接の和は、$△\text{ABD}$の内接の和から、$∠\text{CBD}=α, ∠\text{CDB}=β$を引き、大きい方の$∠\text{BCD}$を加えることで求めることができます。

$△\text{CBD}$の内角$∠\text{BCD}$は

$$∠ \text{BCD}=180°-(\alpha+\beta)$$

したがって、大きい方の$∠\text{BCD}$は

$$\begin{align*}∠ \text{BCD}_{big}&=360°-\left\{180°-(\alpha+\beta)\right\}\\[0.5em]&=180°+\alpha+\beta\end{align*}$$

よって、凹四角形$\text{ABCD}$の内角の和は

$$\begin{align*}&180°-(\alpha+\beta)+∠ \text{BCD}_{big}\\[0.5em]=&180°-(\alpha+\beta)+(180°+\alpha+\beta)\\[0.5em]=&360°\end{align*}$$

であることがわかります。

　この方法を他の凹部のある多角形に対して使用しても、凹部のない多角形と内角の和が変わらないことがわかります。

図3　三角形に分割

　また、対角線を引いて2つの三角形に分割することでも内角の和が三角形の内角の和$180°$の2倍の$360°$であることがわかります。