鋭角の1つが15°の直角三角形の面積は？

鋭角の1つが$15°$、斜辺の長さが$12$の直角三角形

「上図の$△\text{ABC}$の面積を求めよ。」

このような問題はどのように解けばよいでしょうか？

図1　$△\text{A'BC}$を追加

$\text{BC}$を対称軸として点$\text{A}$に線対称な点$\text{A'}$をおき、$△\text{ABC}$に合同な$△\text{A'BC}$を描き加えます。

図2　$△\text{AA'C}$に$\text{AD}$を引く

$△\text{AA'C}$は$\text{AC}=\text{A'C}$で頂角$∠\text{ACA'}=30°$の二等辺三角形です。この三角形は等辺の長さがわかれば面積を求めることができる三角形です。

関連：1つの辺の長さがわかれば面積が求められる特殊な三角形

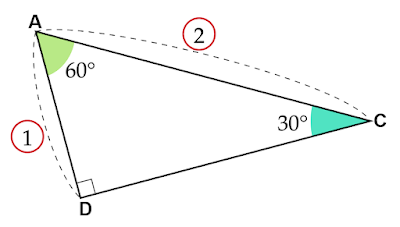
点$\text{A}$から$\text{A'C}$に対して垂線をおろし、$\text{A'C}$との交点を$\text{D}$とします。$\text{A'C}$を底辺とすると$\text{AD}$は高さとなるので、$\text{AD}$の長さがわかれば$△\text{AA'C}$の面積を求めることができます。

図3　$△\text{ACD}$

ここで、$△\text{ACD}$に着目すると$∠\text{ACD}=30°, ∠\text{CAD}=60°$の直角三角形なので、$\text{AC}:\text{AD}=2:1$となります。$\text{AC}=12$なので

\begin{align*}12:\text{AD}&=2:1\\[0.5em]2\text{AD}&=12\\[0.5em]\text{AD}&=6\end{align*}

であるとわかります。

したがって、$△\text{AA'C}$の面積は

\begin{align*}△\text{AA'C}&=\frac{1}{2}\text{A'C}\cdot \text{AD}\\[0.5em]&=\frac{1}{2}\text{AC}\cdot \text{AD}\\[0.5em]&=\frac{1}{2}\cdot 12\cdot 6\\[0.5em]&=\underline{36}\end{align*}

$△\text{ABC}$の面積は$△\text{AA'C}$の面積の半分なので

\begin{align*}△\text{ABC}&=\frac{1}{2}△\text{AA'C}\\[0.5em]&=\frac{1}{2}\cdot 36\\[0.5em]&=\underline{18}\end{align*}

となります。