交差したはしごの問題（Crossed ladders problem）の高さの関係

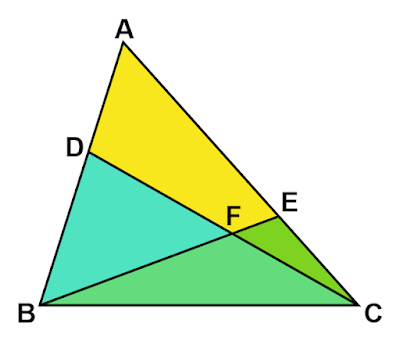
　日本語版がないWikipediaの"Crossed ladders problem"にある高さの関係について調べてみました。

図1　交差したはしごの高さ

　直角三角形ABCとBCを共有する直角三角形DBCがあります。ACとDBの交点EからBCに垂線をおろし、BCとの交点をFとします。
このときAB、DC、EFの長さをそれぞれ$a,b,h$とすると以下のような関係があります。
\[\frac{1}{h}=\frac{1}{a}+\frac{1}{b}\]

なぜこのような関係が成り立つのでしょうか？

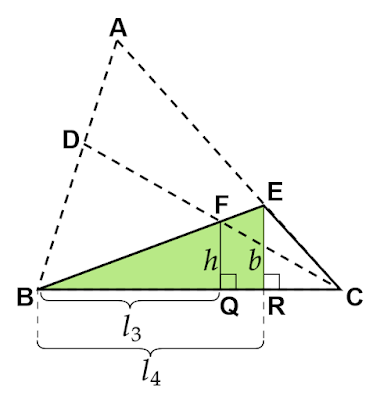
　図1のBC、FC、BFの長さを$l,l_1,l_2$とし、△ABCと△EFCについて考えます。

図2　△ABCと△EFC

この2つの三角形は相似なので、それぞれの三角形の2辺の比は等しくなります。

\begin{equation}l:a=l_1:h\end{equation}

次に△DBCと△EBFについて考えます。

図3　△DBCと△EBF

この2つの三角形も相似なので、それぞれの三角形の2辺の比は等しくなります。

\begin{equation}l:b=l_2:h\end{equation}

　(1)、(2)を比の値にすると

\begin{align}\begin{aligned}(1)\\ \frac{l}{a}&=\frac{l_1}{h}\end{aligned}\\ \begin{aligned}(2)\\ \frac{l}{b}&=\frac{l_2}{h}\end{aligned}\end{align}

(3)と(4)を足して

\begin{align*}\frac{l}{a}+\frac{l}{b}&=\frac{l_1}{h}+\frac{l_2}{h}\\ \\ &=\frac{l_1+l_2}{h}\end{align*}

ここで、$l=l_1+l_2$なので

\[\frac{l}{a}+\frac{l}{b}=\frac{l}{h}\]

両辺を$l$で割って左右を入れ替えれば

\begin{equation}\large{\frac{1}{h}=\frac{1}{a}+\frac{1}{b}}\end{equation}

を導くことができました。

　BCを共通する底辺としたとき、$a$を高さとする三角形は△ABC、$b$を高さとする三角形は△DBC、$h$を高さとする三角形は△EBCであることを踏まえ、(5)の両辺を$\dfrac{1}{2}l$で割ると

\begin{equation}\frac{1}{△EBC}=\frac{1}{△ABC}+\frac{1}{△DBC}\end{equation}

が成り立ちます。

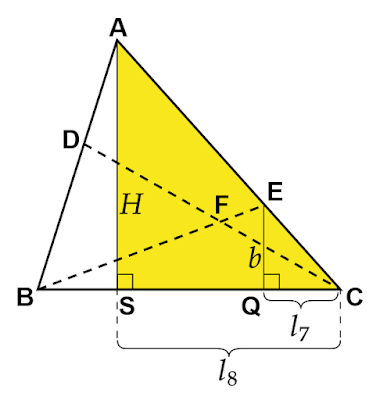
図4　高さが不明な場合

また、図4のようにAB、DC、EFがBCに垂直でないものの平行である場合でも(5)は成り立ちます。△ABC、△DBC、△EBCの高さは$a,b,h$に比例するため(6)も成り立ちます。

　Wikipediaの同ページに"Extended crossed ladders theorem（拡張した交差したはしごの定理）"という項目があります。

図5　拡張した交差したはしごの定理

図5のように△ABCに頂点CからABへ線を引きその交点をD、頂点BからACへ線を引きその交点をEとし、CD、BEの交点をFとしたとき、以下のような関係があります。

\[\frac{1}{△ABC}+\frac{1}{△FBC}=\frac{1}{△DBC}+\frac{1}{△EBC}\]

これを(5)の証明と同様な流れで示すことができます。

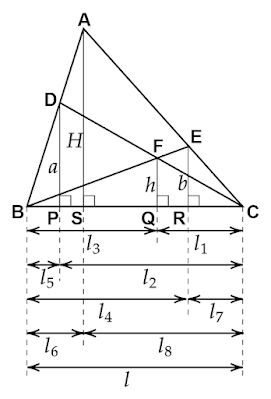
図6　各垂線と底辺の長さ

点D、F、E、AからBCへ垂線をおろし、BCとの交点をそれぞれP、Q、R、Sとします。
各垂線の長さは$DP=a,ER=b,FQ=h,AS=H$とし、$BC=l$として各線分の長さを$QC=l_1,PC=l_2,BQ=l_3,BR=l_4,BP=l_5,BS=l_6,RC=l_7,SC=l_8$とします。
ごちゃごちゃしているので図6にまとめました。

△DPCと△FQCについて考えます。

図7　△DPCと△FQC

これら三角形は相似なので、2辺の比は等しくなります。

\begin{equation}l_1:h=l_2:a\end{equation}

次は△EBRと△FBQについて考えます。

図8　△EBRと△FBQ

これら三角形は相似なので、2辺の比は等しくなります。

\begin{equation}l_3:h=l_4:b\end{equation}

△ABSと△DBPについて考えます。

図9　△ABSと△DBP

これら三角形は相似なので、2辺の比は等しくなります。

\begin{equation}l_6:H=l_5:a\end{equation}

△ASCと△ERCについて考えます。

図10　△ASCと△EQC

これら三角形は相似なので、2辺の比は等しくなります。

\begin{equation}l_8:H=l_7:b\end{equation}

(7)、(8)、(9)、(10)を比の値にすると

\begin{align}\begin{aligned}(7)\\ \frac{l_1}{h}&=\frac{l_2}{a}\end{aligned}\\ \begin{aligned}(8)\\ \frac{l_3}{h}&=\frac{l_4}{b}\end{aligned}\\ \begin{aligned}(9)\\ \frac{l_6}{H}&=\frac{l_5}{a}\end{aligned}\\ \begin{aligned}(10)\\ \frac{l_8}{H}&=\frac{l_7}{b}\end{aligned}\end{align}

(11)、(12)、(13)、(14)を足すと

\begin{align*}\frac{l_1}{h}+\frac{l_3}{h}+\frac{l_6}{H}+\frac{l_8}{H}&=\frac{l_2}{a}+\frac{l_4}{b}+\frac{l_5}{a}+\frac{l_7}{b}\\ \\ \frac{l_6+l_8}{H}+\frac{l_1+l_3}{h}&=\frac{l_2+l_5}{a}+\frac{l_4+l_7}{b}\end{align*}

図6より

\[l=l_1+l_3=l_2+l_5=l_4+l_7=l_6+l_8\]

なので、

\[\frac{l}{H}+\frac{l}{h}=\frac{l}{a}+\frac{l}{b}\]

両辺を$l$で割ると

\[\frac{1}{H}+\frac{1}{h}=\frac{1}{a}+\frac{1}{b}\]

となります。

$H,h,a,b$はそれぞれ△ABC、△FBC、△DBC、△EBCの高さとなるので、両辺を$\dfrac{1}{2}l$で割ると

\[\large{\frac{1}{△ABC}+\frac{1}{△FBC}=\frac{1}{△DBC}+\frac{1}{△EBC}}\]

が成り立つことがわかります。

外部リンク：Crossed ladders problem - Wikipedia