方べきの定理はなぜ成り立つ？ ~ 数学について考えてみる

Processing math: 100%

2022年1月6日

方べきの定理はなぜ成り立つ？

PLUMBAGO

　なぜ方べきの定理が成り立つのか調べてみました。

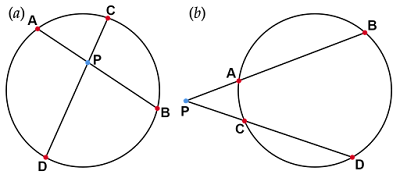
方べきの定理1

　方べきの定理とは、円の2本の弦

$\text{AB, CD}$ 、またはそれらの延長の交点

$\text{P}$ から円周上の各点の距離の関係を表した定理で、上図の

$\text{(a), (b)}$ の場合は、

$\large \text{AP}\cdot\text{BP}=\text{CP}\cdot\text{DP}$

が成り立ちます。

方べきの定理2

上図

$\text{(c)}$ のように接線

$\text{AP}$ と弦

$\text{BC}$ の延長が点

$\text{P}$ で交わっている場合は

$\large{\text{AP}}^2=\text{BP}\cdot\text{CP}$

が成り立ちます。

　これらが成立することを証明してみます。

$\text{(a)}$

方べきの定理　証明1

　

$\text{AC, BD}$ を引き、

$△\text{PAC}$ と

$△\text{PDB}$ について考えます。

円周角の定理より

$\begin{align*}∠\text{PAC}&=∠\text{PDB}\\[1em]∠\text{PCA}&=∠ \text{PBD}\end{align*}$

2組の角がそれぞれ等しいので

$△\text{PAC}$ と

$△\text{PDB}$ は相似であることがわかります。

その相似比より

$\text{AP}:\text{DP}=\text{CP}:\text{BP}$ が成り立つ、すなわち

$\text{AP}\cdot\text{BP}=\text{CP}\cdot\text{DP}$

が成り立つことがわかります。

$\text{(b)}$

方べきの定理　証明2

　

$\text{AC, BD}$ を引き、

$△\text{PAC}$ と

$△\text{PDB}$ について考えます。

円に内接する四角形の対角の性質より

$\begin{align*}∠\text{PAC}&=∠\text{PDB}\\[1em] ∠\text{PCA}&=∠ \text{PBD}\end{align*}$

2組の角がそれぞれ等しいので、

$△\text{PAC}$ と

$△\text{PDB}$ は相似であることがわかります。

その相似比より

$\text{AP}:\text{DP}=\text{CP}:\text{BP}$ が成り立つ、すなわち

$\text{AP}\cdot\text{BP}=\text{CP}\cdot\text{DP}$

が成り立つことがわかります。

$\text{(c)}$

方べきの定理　証明3

　

$\text{AB, AC}$ を引き、

$△\text{PAB}$ と

$△\text{PCA}$ について考えます。

共通な角なので、

$∠\text{APB}=∠\text{CPA}$ です。
接弦定理より

$∠\text{PAB}=∠\text{PCA}$ です。
2組の角がそれぞれ等しいので

$△\text{PAB}$ と

$△\text{PCA}$ は相似であることがわかります。

その相似比より

$\text{AP}:\text{CP}=\text{BP}:\text{AP}$ が成り立つ、すなわち

$\text{AP}^2=\text{BP}\cdot\text{CP}$

が成り立つことがわかります。

以上より方べきの定理が成立することがわかりました。

Share: