星型五角形の角度を求める

「上の角度$a,b,c$を求めよ。」

このような問題はどのように解けばよいでしょうか？

角度$a$

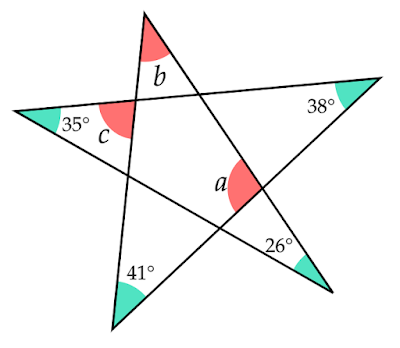
　角度$a$は上図の赤線のように補助線を引き、緑色と斜線部の三角形を利用して求めます。黄色で示した角の和を$y$とおくと、緑色の三角形の内角の和は$180°$なので

$$\begin{equation}35°+38°+26°+y=180°\end{equation}$$

となります。

また、斜線部の三角形の内角は黄色で示した角以外のもう1つの角は対頂角の性質より$a$と等しくなるので、その和は$180°$なので

$$\begin{equation}a+y=180°\end{equation}$$

$(1)$と$(2)$を比較すると和が$180°$であることと$y$を加えていることが共通していることから、それ以外の部分が等しくなるため

$$a=35°+38°+26°=99°$$

であることがわかります。

角度$b$

　角度$b$は上図のように緑色の三角形部分に着目して求めます。

三角形の内角の和は$180°$なので

$$b+99°+41°=180°$$

となります。このことから

$$b=180°-99°-41°=40°$$

であるとわかります。

　また、星型五角形の先端部の角度の和は$180°$であることからも

$$\begin{align*}b&+35°+41°+26°+38°=180°\\[0.5em]b&=180°-35°-41°-26°-38°\\[0.5em]&=40°\end{align*}$$

のように求めることができます。

関連：星型五角形の先端の角度の和はなぜ180°なのか？

角度$c$

　角度$c$は角度$a$と同じように求めることができます。

上図の緑色の部分より紫色で示した角$p$は

$$p=26°+35°+40°=101°$$

と求めることができ、$c+p=180°$なので、

$$\begin{align*}c&=180°-p\\[0.5em]&=180°-101°\\[0.5em]&=79°\end{align*}$$

であることがわかります。

　また、上図の三角形に着目すれば外角の定理より外角と隣接しない三角形の内角の和が等しくなるので

$$c=41°+38°=79°$$

と求めることができます。

関連：外角の定理