「次の不等式の表す領域を図示せよ。
(1)$\large y\geqq -2x+3$
(2)$\large y<x^2+4x+1$
(3)$\large x^2+y^2<4$」
このような問題はどのように解けばよいでしょうか?
(1)$y\geqq -2x+3$
まずは$y=-2x+3$のグラフを描きます。
この直線上にある点の座標は$(x,-2x+3)$と表されます。
$y\geqq-2x+3$はyの値が$-2x+3$以上、すなわち直線$y=-2x+3$上の点とy座標が同じかより大きい点が存在する部分ということなので、$y\geqq-2x+3$の示す領域は上図の赤い部分となります。直線$y=-2x+3$上の点とy座標が同じ点が含まれるということは、境界となる直線$y=-2x+3$も含まれます。
(2)$y<x^2+4x+1$
(1)と同様に$y=x^2+4x+1$のグラフを描きます。
この曲線上の点の座標は$(x,x^2+4x+1)$と表されます。
$y<x^2+4x+1$はyの値が$x^2+4x+1$より小さい、すなわち曲線上の点よりy座標が小さい点の存在する部分ということなので、$y<x^2+4x+1$の示す領域は上図の緑の部分となります。ただし、境界となる曲線$y=x^2+4x+1$は含みません。
$y>f(x)$のようにyについての不等式で表される領域は$y=f(x)$上の点よりy座標が大きい部分か小さい部分となります。不等式に使われている不等号が等号付き不等号のときに境界となる$y=f(x)$が領域に含まれます。
(3)$x^2+y^2<4$
$y$についての不等式でない場合は図形的に考えます。
まず$x^2+y^2=4$について考えると、中心$(0,0)$からの距離が$2$である点の集まりであることを三平方の定理を利用して表しています。
したがって、$x^2+y^2<4$は原点$(0,0)$からの距離が$2$未満となる点が存在する部分なので、$x^2+y^2<4$の示す領域は上図の青い部分となります。ただし、境界となる円$x^2+y^2=4$は含みません。
Share:
https://p-suugaku.blogspot.com/2022/09/futoushiki-ryouiki.html不等式と領域 どの部分?
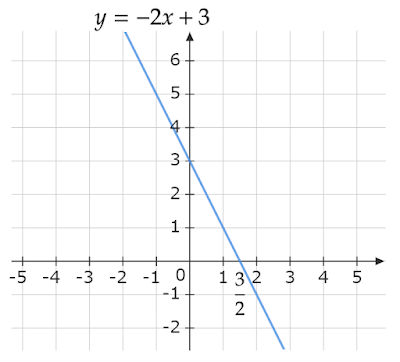
.png)
.png)
.png)
.png)
.png)
.png)



