(1)$\large\vec{a}=(-5,-7),\vec{b}=(-1,2)$
(2)$\large\vec{a}=(4,-1),\vec{b}=(3,4)$」
もう1つのベクトルと垂直な成分を求めるにはベクトルの内積を利用します。
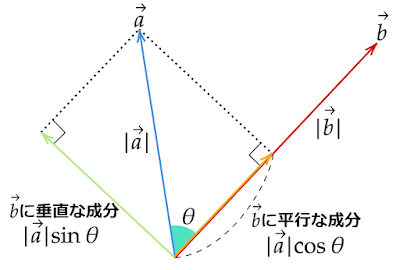
$\vec{a}$は$\vec{b}$に平行なベクトルと$\vec{b}$に垂直なベクトルを合成してできたベクトルと考えます。
ここでいう成分とは、座標平面のx軸、y軸の向きを基準にしたベクトル成分のことではなく、$\vec{b}$の向きを基準にしたもののことです。
ここで、ベクトルの内積の定義式より$\cos\theta$は
\[\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\]
となるので、$\vec{b}$に平行な成分は
\[|\vec{a}|\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|}\]
と書けます。
この成分に$\vec{b}$の向きを付け加えれば$\vec{b}$に平行なベクトルを表すことができます。そこで登場するのが$\vec{b}$の単位ベクトルです。
単位ベクトルは大きさが$1$のベクトルです。これに実数を掛ければ同じ向きを持つ任意のベクトルをつくることができます。
$\vec{b}$と同じ向きを持つ単位ベクトルをつくるには$\vec{b}$を自身の大きさで割れば良いので$\dfrac{\vec{b}}{|\vec{b}|}$となります。
したがって、$\vec{b}$に平行なベクトルは
\[\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|}\cdot\frac{\vec{b}}{|\vec{b}|}=\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\vec{b}\]
となります。
$\vec{a}$は$\vec{b}$に平行なベクトルと$\vec{b}$に垂直なベクトルの和として考えているので、$\vec{a}$から$\vec{b}$に平行なベクトルを引いた
\[\vec{a}-\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\vec{b}\]
が$\vec{a}$の$\vec{b}$に垂直なベクトルとなります。
これを利用して問題を解きます。
(1)$\vec{a}=(-5,-7),\vec{b}=(-1,2)$
内積と$\vec{b}$の大きさはそれぞれ
\begin{align*}\vec{a}\cdot\vec{b}&=(-5)\cdot(-1)+(-7)\cdot2\\[0.5em]&=-9\\[1.5em]|\vec{b}|&=\sqrt{(-1)^2+2^2}\\[0.5em]&=\sqrt{5}\end{align*}
となるので、$\vec{a}$の$\vec{b}$に垂直なベクトル成分は
\begin{align*}\vec{a}-\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\vec{b}&=(-5,-7)-\frac{-9}{(\sqrt{5})^2}(-1,2)\\[0.5em]&=(-5,-7)+\frac{9}{5}(-1,2)\\[0.5em]&=(-5,-7)+\left(-\frac{9}{5},\frac{18}{5}\right)\\[0.5em]&=\left(-\frac{34}{5},-\frac{17}{5}\right)\end{align*}
となります。
(2)$\vec{a}=(4,-1),\vec{b}=(3,4)$
内積と$\vec{b}$の大きさはそれぞれ
\begin{align*}\vec{a}\cdot\vec{b}&=4\cdot3+(-1)\cdot4\\[0.5em]&=8\\[1.5em]|\vec{b}|&=\sqrt{3^2+4^2}\\[0.5em]&=\sqrt{25}\\[0.5em]&=5\end{align*}
となるので、$\vec{a}$の$\vec{b}$に垂直なベクトル成分は
\begin{align*}\vec{a}-\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\vec{b}&=(4,-1)-\frac{8}{5^2}(3,4)\\[0.5em]&=(4,-1)-\left(\frac{24}{25},\frac{32}{25}\right)\\[0.5em]&=\left(\frac{76}{25},-\frac{57}{25}\right)\end{align*}
となります。
Share: