この点は領域に入る？入らない？

「次の不等式が表す領域内に[]内の点は存在するかどうかを調べよ。

(1)$\large y<3x+2\quad[(-1,3)]$

(2)$\large y>-x^2+3x+4\quad[(3,5)]$

(3)$\large \dfrac{x^2}{3}+\dfrac{y^2}{4}\leqq2\quad[(1,-2)]$」

このような問題はどのように解けばよいでしょうか？

　ある点が不等式の表す領域内にあるかどうかを確かめるには、その点の座標を不等式に代入してみて不等式が成立するかどうかで判断します。

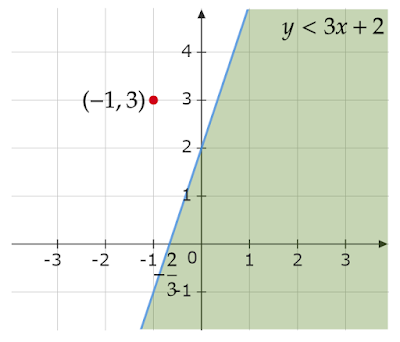
(1)$y<3x+2\quad[(-1,3)]$

　領域内にあるかどうかを確かめたい点は$(-1,3)$なので、$x=-1,y=3$を代入すると

$$\begin{align*}3&<3\cdot(-1)+2\\[0.5em]3&<-1\end{align*}$$

となり、正しい大小関係$3>-1$ではないので、不等式が成り立っていません。

したがって、下図に示すように点$(-1,3)$は$y<3x+2$の領域内にありません。

(2)$y>-x^2+3x+4\quad[(3,5)]$

　$x=3,y=5$を代入すると

$$\begin{align*}5&>-3^2+3\cdot3+4\\[0.5em]5&>4\end{align*}$$

となり、正しい大小関係になっているため、不等式が成り立っています。

したがって、下図に示すように点$(3,5)$は$y>-x^2+3x+4$の領域内にあります。

(3)$\dfrac{x^2}{3}+\dfrac{y^2}{4}\leqq2\quad[(1,-2)]$

　$x=1,y=-2$を代入すると

$$\begin{align*}\frac{1^2}{3}+\frac{(-2)^2}{4}&\leqq2\\[0.5em]-\frac{2}{3}&\leqq2\end{align*}$$

となり、正しい大小関係になっているため、不等式が成り立っています。（$-\frac{2}{3}\leqq2$は”$-\dfrac{2}{3}<2$または$-\dfrac{2}{3}=2$”という意味で、前者が成り立っているので元の不等式も成り立ちます。）

したがって、下図に示すように点$(1,-2)$は$\dfrac{x^2}{3}+\dfrac{y^2}{4}\leqq2$の領域内にあります。

関連：不等式と領域