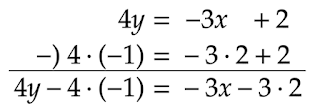「次の不定方程式の整数解をすべて求めよ。
(1)$\large 2x-y=3$
(2)$\large 3x+4y=2$」このような問題はどのように解けばよいでしょうか?
(1)$2x-y=3$
変形をすると
\[y=2x-3\tag{a}\]
直線の方程式になります。
$x$の係数も定数項も整数なので$x$が整数であれば$y$も整数になることがわかります。
このことから、$x=0$を代入すると
このことから、$x=0$を代入すると
\begin{align*}y&=2\cdot0-3\\[0.5em]&=-3\end{align*}
なので、整数解の1つは$x=0,y=-3$であることがわかります。これは$(1)$を直線の方程式と考えたときの直線上の点の座標となります。
他の整数解を求める方法は2つあります。
1. 直線の傾きを利用
1つは直線の方程式の傾きに着目する方法です。
\[(傾き)=\frac{\text{(yの変化量)}}{\text{(xの変化量)}}\]
で求められることを考えると$\text{(a)}$の傾きは$2$であり、分数で表せば
\[2=\frac{2}{1}\]
となります。つまり、$x$が$1$増えれば、それにともない$y$は$2$増えるということです。
したがって、直線上のある点から$x,y$をそれぞれ傾きが示す分だけ増加させれば他の直線上の点の座標がわかります。
$x=0$に$1$を足すと$x=1$、$y=-3$に$2$を足すと$y=-1$となるので、$x=1,y=-1$がもう1つの整数解であることがわかります。
ここで、$x$に$1$、$y$に$2$をそれぞれ足すという工程を何度か繰り返せば整数解が無数につくれることがわかると思います。
これを整数$k$をもちいて、上記の工程を$k$回繰り返したときの整数解は
不定方程式の整数解を求める問題の場合、この一般解が問題の解答となります。
対して、最初に求めた整数解$x=0,y=-3$のように$k$をもちいない、いくつかある整数解のうち1つを表したものを特殊解と呼びます。
これを整数$k$をもちいて、上記の工程を$k$回繰り返したときの整数解は
\[x=0+k=k,\quad y=-3+2k\]
と表すことができます。これはすべての整数解の間にある法則性を$k$という文字を使って表したものなので、$k$に任意の整数を代入することですべての整数解を求めることができます。これを不定方程式の一般解と呼びます。不定方程式の整数解を求める問題の場合、この一般解が問題の解答となります。
対して、最初に求めた整数解$x=0,y=-3$のように$k$をもちいない、いくつかある整数解のうち1つを表したものを特殊解と呼びます。
ちなみに、不定方程式の一般解は1つ目の整数解(特殊解)に何を求めたか?法則性をどのように捉えたかで式の形が変わります。
例えば、$x=1,y=-1$も特殊解の1つなので、これが最初の整数解だった場合、一般解は
例えば、$x=1,y=-1$も特殊解の1つなので、これが最初の整数解だった場合、一般解は
\[x=1+k,\quad y=-1+2k\]
となります。
また、傾き$2$を
\[2=\frac{-2}{-1}\]
すなわち$x$が$1$減ると、それにともない$y$が$2$減ると捉えた場合、一般解は
\[x=-k,\quad y=-3-2k\]
となります。これらもまたすべての整数解を表すことができる一般解です。
2. 連立方程式を利用
もう1つは連立方程式を利用する方法です。
$\text{(a)}$と$\text{(a)}$に特殊解$x=0,y=-3$を代入した式を連立します。このとき、特殊解を代入した式は計算・整理せずにそのままにしておいてください。
\begin{cases}y&=2x-3\\[0.5em]-3&=2\cdot0-3\end{cases}
それぞれの辺を引き、$x,y$それぞれの係数でくくります。
\begin{align*}(y+3)&=2(x-0)\\[0.5em](y+3)&=2x\tag{b}\end{align*}
すると、右辺は$2$を因数に持つから左辺$y-3$は偶数であることがわかります。
このことから、任意の整数$k$をもちいて
\[y+3=2k\]
とおくことができます。これを$y$について解くと
\[y=-3+2k\]
これを$\text{(b)}$に代入して$x$について解くと
\begin{align*}(-3+2k)+3&=2x\\[0.5em]x&=k\end{align*}
となります。
したがって、$x=k,\quad y=-3+2k$が不定方程式の一般解となります。
(2)$3x+4y=2$
(1)と同様に変形すると
\begin{align*}4y&=-3x+2\tag{c}\\[0.5em]y&=\frac{-3x+2}{4}\end{align*}
となります。
$y$が整数であるためには$-3x+2$が4の倍数である必要があるので、これを満たすような整数$x$を探します。
$-3x+2$が4の倍数になるのは$x=2$のときが挙げられ、このとき$y$は
$-3x+2$が4の倍数になるのは$x=2$のときが挙げられ、このとき$y$は
\[y=\frac{-3\cdot2+2}{4}=-1\]
となるので、$x=2,y=-1$が特殊解となります。
一般解を(1)と同様2通りの方法で求めてみます。
1.
さらに変形すると
\[y=-\frac{3}{4}x+\frac{1}{2}\]
となるので、傾きは$-\dfrac{3}{4}$であることがわかります。
2.
$4$と$-3$は互いに素であるにも関わらず等号で結ばれているということは、左辺から見て右辺の$x-2$には$4$が、右辺から見て左辺の$y+1$には$-3$が因数に含まれているはずです。
このことから、$\text{(d)}$の両辺にはそれぞれ因数が$-3$と$4$とそれ以外の$k$が含まれていることになるので、
\[4(y+1)=-3(x-2)=(-3)\cdot4\cdot k\]
と書けます。すると、
\begin{cases}4(y+1)&=(-3)\cdot4\cdot
k\\[0.5em]-3(x-2)&=(-3)\cdot4\cdot k\end{cases}
ということなので、$x,y$それぞれについて解くと
\begin{align*}4(y+1)&=(-3)\cdot4\cdot
k\\[0.5em]y+1&=-3k\\[0.5em]y&=-1-3k\\[1.5em]-3(x-2)&=(-3)\cdot4\cdot
k\\[0.5em]x-2&=4k\\[0.5em]x&=2+4k\end{align*}
したがって、不定方程式の一般解は$x=2+4k,y=-1-3k$となります。
Share:
.png)
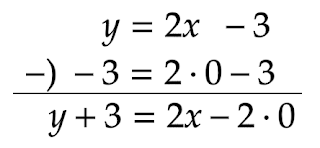
.png)