楕円の長軸と短軸の各部分の長さは？

　楕円$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$の長軸と短軸はx軸とy軸です。
この長軸と短軸そのものの長さや、焦点で区切られた線分の長さはどうなっているのでしょうか？

　まずは長軸と短軸の長さを調べます。

$a>b>0$のとき、長軸の長さはx軸と楕円の交点間の距離なので、この交点の座標を求めます。
x軸は直線$y=0$なので、$y=0$を代入して

$$\begin{align*}\frac{x^2}{a^2}=1\\[0.5em]x^2&=a^2\\[0.5em]x&=\pm a\end{align*}$$

したがって、x軸と楕円の交点は$(-a, 0), (a, 0)$なので長軸の長さは$2a$となります。

同様に短軸の長さは、y軸（$x=0$）と楕円の交点間の距離なので$x=0$を代入して

$$\begin{align*}\frac{y^2}{b^2}&=1\\[0.5em]y^2&=b^2\\[0.5em]y&=\pm b\end{align*}$$

したがって、y軸と楕円の交点は$(0, -b), (0, b)$なので短軸の長さは$2b$となります。

$b>a>0$のときは長軸の長さは$2b$、短軸の長さは$2a$となります。

　長軸上には楕円の焦点があります。この焦点間の距離を調べます。
そのためには一度楕円の定義を振り返ります。楕円の定義は「焦点となる2定点からの距離の和が一定となる点の軌跡」です。この2つの焦点からの距離の和は長軸の長さとなります。
このことから$a>b>0$のとき、楕円の焦点の座標を$(-p, 0), (p, 0)$とおくと2つの焦点からの距離の和、すなわち長軸の長さは$2a$となるので

$$\begin{align*}\sqrt{(x+p)^2+y^2}+\sqrt{(x-p)^2+y^2}&=2a\\[0.5em]\sqrt{(x+p)^2+y^2}&=2a-\sqrt{(x-p)^2+y^2}\end{align*}$$

両辺を2乗して

$$\begin{align*}(x+p)^2+y^2&=4a^2-4a\sqrt{(x-p)^2+y^2}+(x-p)^2+y^2\\[0.5em]4a\sqrt{(x-p)^2+y^2}&=4a^2-4px\\[0.5em]a\sqrt{(x-p)^2+y^2}&=a^2-px\end{align*}$$

両辺を2乗して

$$\begin{align*}a^2\{(x-p)^2+y^2\}&=a^4-2a^2px+p^2x^2\\[0.5em]a^2(x^2-2px+p^2+y^2)&=a^4-2a^2px+p^2x^2\\[0.5em](a^2-p^2)x^2+a^2y^2&=a^4-a^2p^2\\[0.5em](a^2-p^2)x^2+a^2y^2&=a^2(a^2-p^2)\end{align*}$$

両辺を$a^2(a^2-p^2)$で割って

$$\frac{x^2}{a^2}+\frac{y^2}{a^2-p^2}=1$$

楕円の方程式$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$と比較すると

$$b^2=a^2-p^2$$

となり、$p$について解くと

$$\begin{align*}p^2&=a^2-b^2\\[0.5em]p&=\pm\sqrt{a^2-b^2}\end{align*}$$

となるので、焦点の座標は$(-\sqrt{a^2-b^2}, 0), (\sqrt{a^2-b^2}, 0)$、焦点間の距離は$2\sqrt{a^2-b^2}$であることがわかります。

$b>a>0$のときも同様にすれば

$$\begin{align*}\sqrt{x^2+(y+p)^2}+\sqrt{x^2+(y-p)^2}&=2b\\[0.5em]\sqrt{x^2+(y+p)^2}&=2b-\sqrt{x^2+(y-p)^2}\\[0.5em]x^2+(y+p)^2&=4b^2-4b\sqrt{x^2+(y-p)^2}+x^2+(y-p)^2\\[0.5em]b\sqrt{x^2+(y-p)^2}&=b^2-py\\[0.5em]b^2\{x^2+(y-p)^2\}=b^4-2py+p^2y^2\\[0.5em]b^2x^2+(b^2-p^2)y^2&=b^2(b^2-p^2)\\[0.5em]\frac{x^2}{b^2-p^2}+\frac{y^2}{b^2}&=1\end{align*}$$

となるから、$a^2=b^2-p^2$より焦点の座標が$(0, -\sqrt{b^2-a^2}), (0, \sqrt{b^2-a^2})$、焦点間の距離は$2\sqrt{b^2-a^2}$と求まります。

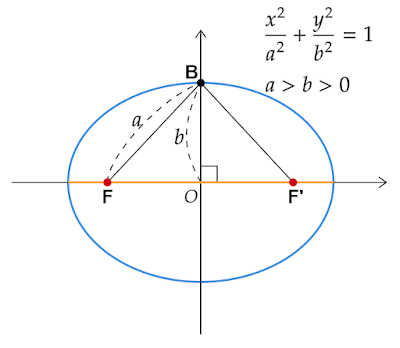
これは楕円のグラフからもわかります。

長軸がx軸のとき、上図のように楕円とy軸の交点、すなわち短軸の端点から各焦点までの距離は等しくなるので長軸の長さの半分の$a$となります。楕円の中心である原点から短軸の端点までの距離は短軸の長さの半分の$b$となります。

原点、焦点、短軸の端点の3点を結ぶと直角三角形ができるので、三平方の定理を利用して原点から焦点までの距離を求めると

$$\begin{align*}\text{BF}^2&=\text{OB}^2+\text{OF}^2\\[0.5em]\text{OF}^2&=\text{BF}^2-\text{OB}^2\\[0.5em]&=a^2-b^2\\[0.5em]\text{OF}&=\sqrt{a^2-b^2}&(\because \text{OF}>0)\end{align*}$$

$\text{F, F'}$はy軸に関して対称なので、焦点の座標は$(-\sqrt{a^2-b^2}, 0), (\sqrt{a^2-b^2}, 0)$、焦点間の距離は$2\sqrt{a^2-b^2}$であることがわかります。

長軸がy軸のときは上図のようになるので、原点から焦点までの距離は

$$\begin{align*}\text{OF}^2&=\text{AF}^2-\text{OA}^2\\[0.5em]&=b^2-a^2\\[0.5em]\text{OF}&=\sqrt{b^2-a^2}&(\because \text{OF}>0)\end{align*}$$

$\text{F, F'}$はx軸に関して対称なので、焦点の座標は$(0, -\sqrt{b^2-a^2}), (0, \sqrt{b^2-a^2})$、焦点間の距離は$2\sqrt{b^2-a^2}$であることがわかります。

まとめると上図のようになります。