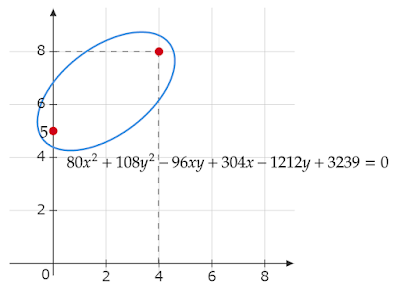
「2定点$A(0,5),B(4,8)$それぞれからの距離の和が$6$である楕円の方程式を求めよ。また、この楕円上のy座標が最小となる点の座標を求めよ。」
このような問題はどのように解けばよいのでしょうか？
.png)
\[\sqrt{x^2+(y-5)^2}+\sqrt{(x-4)^2+(y-8)^2}=6\]
楕円上の点$(x,y)$は常に上式を満たします。
これを変形して楕円の方程式を求めます。
\[\sqrt{x^2+(y-5)^2}=6-\sqrt{(x-4)^2+(y-8)^2}\]
両辺を2乗して
\begin{align*}x^2+(y-5)^2&=36-12\sqrt{(x-4)^2+(y-8)^2}+(x-4)^2+(y-8)^2\\[0.5em]-8x-6y+91&=12\sqrt{(x-4)^2+(y-8)^2}\end{align*}
両辺を2乗して
\begin{align*}&64x^2+36y^2+96xy-1456x-1092y+8281\\
&\quad=144\{(x-4)^2+(y-8)^2\}\\[0.5em]&80x^2+108y^2-96xy+304x-1212y+3239=0\end{align*}
これが求める楕円の方程式となります。
この方程式が描く楕円のy座標が最小となる点を求めるには、楕円の方程式を$y$について降べきの順に並べ替えます。
.png)
\begin{align*}108y^2-96xy-1212y+80x^2+304x+3239&=0\\[0.5em]108y^2-(96x+1212)y+80x^2+304x+3239&=0\end{align*}
これを2次方程式の解の公式を使って$y$について解きます。
\begin{align*}y&=\frac{48x+606\pm\sqrt{(48x+606)^2-108(80x^2+304x+3239)}}{108}\\[0.5em]y&=\frac{6(8x+101)\pm6\sqrt{(8x+101)^2-3(80x^2+304x+3239)}}{6\cdot18}\\[0.5em]y&=\frac{8x+101\pm\sqrt{-176x^2+704x+484}}{18}\\[0.5em]y&=\frac{8x+101\pm2\sqrt{-44x^2+176x+121}}{18}\end{align*}
この式の複号が$+$の場合は楕円の上側、$-$の場合は楕円の下側を表します。
.png)
また、楕円の方程式において$x$の値は根号部分が実数でなければならない、すなわち$-44x^2+176x+121\geqq0\quad\cdots(1)$を満たす必要があります。
$(1)$を解くと$x$の変域は
$(1)$を解くと$x$の変域は
\begin{align*}4x^2-16x-11&\leqq0\\[0.5em]4x^2-16x-11&=0において\\
x&=\frac{8\pm\sqrt{(-8)^2-4\cdot(-11)}}{4}\\[0.5em]&=\frac{4\pm3\sqrt{3}}{2}なので\\[0.5em]\frac{4-3\sqrt{3}}{2}&\leqq
x\leqq\frac{4+3\sqrt{3}}{2}\end{align*}
であるとわかります。
楕円のy座標が最小となる点は楕円の下側に存在するため、
$x$で微分すると
\[y=\frac{8x+101-2\sqrt{-44x^2+176x+121}}{18}\]
に着目します。$x$で微分すると
\begin{align*}y'&=\frac{1}{18}\left(8x+101-2\sqrt{-44x^2+176x+121}\right)'\\[0.5em]y'&=\frac{1}{18}\left\{8-2\cdot\frac{(-44x^2+176x+121)'}{2\sqrt{-44x^2+176x+121}}\right\}\\[0.5em]y'&=\frac{1}{18}\left(8+\frac{88x-176}{\sqrt{-44x^2+176x+121}}\right)\\[0.5em]y'&=\frac{4}{9}+\frac{44x-88}{9\sqrt{-44x^2+176x+121}}\end{align*}
$y'=0$のときの$x$は
\begin{align*}&\frac{4}{9}+\frac{44x-88}{9\sqrt{-44x^2+176x+121}}=0\\[0.5em]&1+\frac{11x-22}{\sqrt{-44x^2+176x+121}}=0\\[0.5em]&\frac{11x-22}{\sqrt{-44x^2+176x+121}}=-1\\[0.5em]&11x-22=-\sqrt{-44x^2+176x+121}\end{align*}
両辺を2乗すると、$(1)$より
\begin{align*}121x^2-484x+484&=-44x^2+176x+121\\[0.5em]165x^2-660x+363&=0\\[0.5em]5x^2-20x+11&=0\\[0.5em]x&=\frac{10\pm\sqrt{(-10)^2-5\cdot11}}{5}\\[0.5em]&=\frac{10\pm3\sqrt{5}}{5}\end{align*}
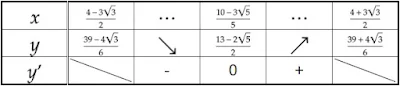
代入して確かめてみると$y'=0$を満たす$x$は$x=\dfrac{10-3\sqrt{5}}{5}$だけです。
増減表は以下のようになり、$x=\dfrac{10-3\sqrt{5}}{5}$で極小値$\dfrac{13-2\sqrt{5}}{2}$をとり、これが最小値となることがわかります。
したがって、問題の答えは
\begin{align*}80x^2+108y^2-96xy+304x-1212y+3239=0,\\
(\frac{10-3\sqrt{5}}{5},\frac{13-2\sqrt{5}}{2})\end{align*}
となります。
Share:
