円を3等分する平行線はどこに引く？ ~ 数学について考えてみる

　円に平行な直線を2本引いて円の面積を3等分したいとき、2本の平行な直線はそれぞれどこに引けばよいでしょうか？

　直線$l$を円の中心$\text{O}$から$x$だけ離れた位置に引いた場合を考えます。

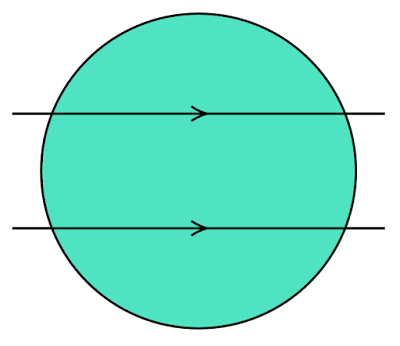
直線$l$が円$\text{O}$の面積を3等分する平行な2本の直線の1本であった場合、直線$l$と円$\text{O}$の2つの交点をそれぞれ$\text{A, B}$としたときの弓形$\text{AB}$の面積は円$\text{O}$の面積の$\dfrac{1}{3}$となります。

円は線対称な図形なので、もう1本の直線$m$を中心$\text{O}$から直線$l$とは逆方向に$x$だけ離れた位置に引くことで直線$m$と円$\text{O}$の2つの交点をそれぞれ$\text{C, D}$としたときの弓形$\text{CD}$の面積もまた、円$\text{O}$の面積の$\dfrac{1}{3}$となります。
あとは、円の中心$\text{O}$からの距離$x$が分かれば、円の面積を3等分できます。

　$x$を求めるために、まずは弓形$\text{AB}$の面積について考えます。

弓形$\text{AB}$の面積はおうぎ形$\text{OAB}$の面積から$△\text{OAB}$の面積を引いたものとなります。

円$\text{O}$の半径が$r$、弧$\text{AB}$に対する中心角が$θ\mathrm[rad]$のとき、おうぎ形$\text{AB}$の面積は$おうぎ形\text{AB}=\dfrac{θr^2}{2}$と表されます。
また、$△\text{OAB}$の面積は$△\text{OAB}=\dfrac{r^2\sinθ}{2}$となります。

したがって、弓形$\text{AB}$の面積は

\begin{align*}弓形\text{AB}&=\frac{\theta r^2}{2}-\frac{r^2\sinθ}{2}\\[0.5em]&=\frac{r^2}{2}(\theta-\sin\theta)\end{align*}

となります。

ここで、円$\text{O}$の面積は$\pi r^2$なので、3等分してできる各図形の面積は$\dfrac{\pi r^2}{3}$となります。

以上より、方程式

\begin{equation}\frac{r^2}{2}(\theta-\sin\theta)=\frac{\pi r^2}{3}\end{equation}

を満たす$θ$が弓形$\text{AB}$が円$\text{O}$の$\dfrac{1}{3}$の面積をもつときの弧$\text{AB}$に対する中心角となります。

変形して簡単な形にすると

\begin{equation}\theta-\sin\theta-\frac{2\pi}{3}=0\end{equation}

となりますが、この方程式を解いて$θ$の値を求めるのは大変なのでニュートン法により近似値を求めます。

　ニュートン法で$θ$の近似値が分かれば、$x$の値も近似値として求められます。

$△\text{OAB}$は二等辺三角形なので、頂角$∠\text{AOB}$の二等分線は頂点$\text{O}$から底辺$\text{AB}$へおろした垂線となります。

垂線の足を$\text{M}$とすると、線分$\text{OM}$の長さは点$\text{O}$から直線$l$の距離に等しく$x$となります。

ここで、$△\text{OAM}$に着目すれば$\text{OA}=r,∠\text{AOM}=\dfrac{θ}{2}$であることと三角比より

\begin{equation}x=r\cos\frac{\theta}{2}\end{equation}

となり、これで$x$の値がわかります。

ちなみに、線分$\text{AB}$の長さは

\begin{align*}\text{AB}&=2\text{AM}\\[0.5em]\text{AB}&=2r\sin\frac{\theta}{2}\tag3\end{align*}

で求めることができます。

　では、ニュートン法で弧$\text{AB}$に対する中心角$θ$の近似値を求めてみましょう。

$f(θ)=θ-\sinθ-\dfrac{2\pi}{3}$を考えます。
ニュートン法で$f(θ)=0$を満たす$θ$の近似値を求めるには、$f'(θ)$と$θ_n$における接線のθ切片$θ_{n+1}$を表す式、$θ$に最初に代入する値$θ_0$が必要になります。

$f'(θ)$は

\[f'(\theta)=1-\cos\theta\]

$θ_{n+1}$を表す式は

\[\theta_{n+1}=\theta_n-\frac{f(\theta_n)}{f'(\theta_n)}\]

をもちいます。
ちなみに$θ_{n+1}$を表す式に$f(θ_n),f'(θ_n)$に代入すれば

\begin{align*}\theta_{n+1}&=\theta_n-\frac{\theta_n-\sin\theta_n}{1-\cos\theta_n}\\[0.5em]&=\frac{\sin\theta_n-\theta_n\cos\theta_n}{1-\cos\theta_n}\end{align*}

とも書けます。

$θ_0$は、$f(θ)=0$を満たす$θ$付近の値をとれば良いので$θ_0=\dfrac{2\pi}{3}$とします。

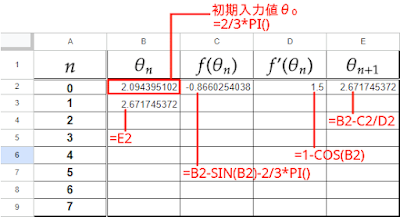
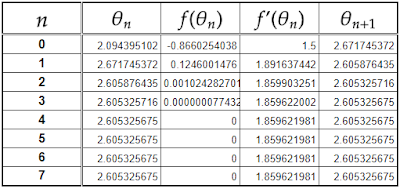
これらを利用して表計算ソフトで計算します。

セルへの入力例は下図（残りのセルは上のセルからオートフィル機能で埋めます。）、