定数a,bについてa<bのとき、a^2とb^2の大小関係はどうなるでしょうか？
5つの場合に分けて考えてみます。
1. a>0のとき
0<a<bということなので、a,bともに正の数の場合です。
a<bの両辺にaを掛けると
また、a<bの両辺にbを掛けると
\begin{equation}a^2<ab\end{equation}
となります。また、a<bの両辺にbを掛けると
\begin{equation}ab<b^2\end{equation}
となります。
(1),(2)よりa^2<ab<b^2、すなわち
a^2<b^2
であることがわかります。
2. a=0のとき
0=a<bということなので、aが0、bは正の数の場合です。
a<bの両辺にaを掛けると
a<bの両辺にbを掛けると
\begin{equation}a^2=ab=0\end{equation}
となります。a<bの両辺にbを掛けると
\begin{equation}(0=)ab<b^2\end{equation}
となります。
(3),(4)より(0=)a^2=ab<b^2、すなわち
a^2<b^2
であることがわかります。
1.、2.より0\leqq a<bのときa^2<b^2が成り立ちます。
3. a<0<bのとき
aとbがそれぞれ負の数と正の数に別れている場合です。
この場合はさらに3つの場合分けが必要となります。
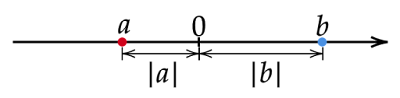
3-1. |a|<|b|のとき
絶対値の性質より0<|a|<|b|なので、1.の場合より
\begin{equation}|a|^2<|b|^2\end{equation}
が成り立ちます。
また、|x|^2=x^2より(5)は
a^2<b^2
となることがわかります。
3-2. |a|=|b|のとき
.png)
このとき|a|=|b|の両辺を2乗して
\begin{equation}|a|^2=|b|^2\end{equation}
となります。
また、|x|^2=x^2より(6)は
a^2=b^2
となることがわかります。
3-3. |a|>|b|のとき
.png)
0<|b|<|a|ということなので、1.の場合より
\begin{equation}|b|^2<|a|^2\end{equation}
が成り立ちます。
また、|x|^2=x^2より(7)は
a^2>b^2
となることがわかります。
3.の場合、a^2とb^2の大小関係を知るためにはaとbそれぞれの絶対値の大小関係を知らなければなりません。
4. b=0のとき
a<b=0ということなので、aは負の数でbが0の場合です。
a<bの両辺にaを掛けると
a<bの両辺にbを掛けると
\begin{equation}a^2>ab=0\end{equation}
となります。a<bの両辺にbを掛けると
\begin{equation}ab=b^2=0\end{equation}
となります。
(8),(9)よりa^2>ab=b^2(=0)、すなわち
a^2>b^2
であることがわかります。
5. b<0のとき
a<b<0ということなので、a,bともに負の数の場合です。
a<bの両辺にaを掛けると
a<bの両辺にbを掛けると
\begin{equation}a^2>ab\end{equation}
となります。a<bの両辺にbを掛けると
\begin{equation}ab>b^2\end{equation}
となります。
(10),(11)よりa^2>ab>b^2、すなわち
a^2>b^2
であることがわかります。
4.、5.よりa<b\leqq0のときa^2>b^2が成り立ちます。
なお、(8),(10),(11)において不等号の向きが変わっているのは両辺に掛けたものが負の数であるためです。
aとbの絶対値に着目すると
1.、2.、3-1.のとき、すなわち|a|<|b|のとき
a^2<b^2
3-2.のとき、すなわち|a|=|b|のとき
a^2=b^2
3-3.、4.、5.のとき、すなわち|a|>|b|のとき
が成り立っていることがわかります。
a^2>b^2
Share:
