不等式に対して行う基本的な操作は両辺に同じ数を足す、引く、掛ける、割るの4つとなります。
この操作を数直線で見るとどのように見えるでしょうか?
例として定数$a,b$をもちいた不等式
\[a<b\]
に対し基本的な操作を行います。
不等式$a<b$とは$a$は$b$より小さいことを表す式で、数直線で表すと以下のようになります。
右方向を正とする数直線において$a$の点は$b$の点より左に位置しています。
この位置関係が不等式の表すものとなっています。
足す
両辺に定数$c$を加えると
\begin{equation}a+c<b+c\end{equation}
となります。
この操作では数直線においては以下のような変化が起きています。
$a$の点、$b$の点ともに数直線の方向に$c$だけ平行移動します。(上図は$c$が正の定数である場合)
平行移動では2点の位置関係が変わることはないので、$(1)$が成り立つことがわかります。
引く
両辺から定数$c$を引くと
\begin{equation}a-c<b-c\end{equation}
となります。
この操作では上の数直線においては以下のような変化が起きています。
$a$の点、$b$の点ともに数直線の方向に$-c$だけ平行移動します。$c$を加えた場合とは逆方向への平行移動となります。(上図は$c$が正の定数である場合)
$c$を加えた場合同様、平行移動では2点の位置関係が変わることはないので、$(2)$が成り立つことがわかります。
ここからは数直線を2本使い、座標平面で表します。
掛ける
両辺に定数$c$を掛けるとき、3つの場合に分かれます。
$c$が正の定数のとき
$c$が正の定数、すなわち$c>0$のとき
\begin{equation}ac<bc\end{equation}
となります。
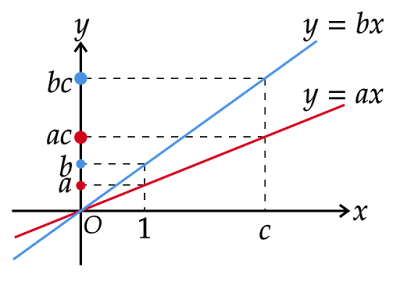
この操作を座標平面で見ると以下のようになります。
これら直線の方程式の$x$が両辺に掛ける数、$y$がその積にあたります。
すなわち、不等式の両辺に$c$を掛けるという操作は、$x$が$1$から$c$に変化することを意味し、その大小関係はそれらの点のy座標に表れることになります。
$x=1$における2つの直線上の点はそれぞれ$(1,a),(1,b)$となります。これら2点を比較すると、不等式$a<b$より点$(1,b)$のほうがy座標が大きいので、点$(1,a)$よりも上に位置します。
これはつまり、直線の傾きは$y=bx$のほうが大きく、$y=ax$より右上がりの直線であるということです。
次は$x=c$における2つの直線上の点の座標を求めてみます。
すると、それぞれ$(c,ac),(c,bc)$となります。$c>0$より、これらの点はx軸の正の部分$x>0$に存在しています。
直線の傾きと点の存在範囲より、点$(c,bc)$のほうが点$(c,ac)$よりも上に位置しています。
したがって、2点のy座標の大小関係より$(3)$が成り立つことがわかります。
$c=0$のとき
$c=0$のとき、両辺とも$0$になります。したがって、
\[ac=bc=0\]
となります。
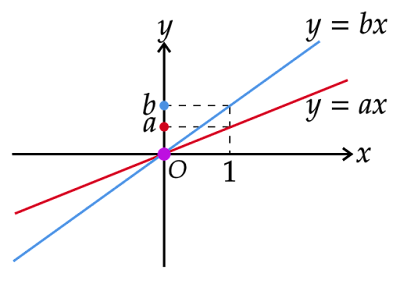
これは座標平面において$x=0$における2つの直線$y=ax,y=bx$の点のy座標がどちらも$0$、すなわち原点であることからもわかります。
$c$が負の定数のとき
$c$が負の定数、すなわち$c<0$のとき
\begin{equation}ac>bc\end{equation}
となります。
この操作を座標平面で見ると以下のようになります。
$c$が正の定数のときと同様、$x=c$における2つの直線$y=ax,y=bx$上の点$(c,ac),(c,bc)$について考えます。
$c<0$より2点はx軸の負の部分$x<0$に存在しています。
直線の傾きと点の存在範囲より、点$(c,ac)$のほうが点$(c,bc)$よりも上に位置しています。
したがって、2点のy座標の大小関係より$(4)$が成り立つことがわかります。
割る
両辺に定数$c$を割るとき、2つの場合に分かれます。
$c$が正の定数のとき
$c$が正の定数、すなわち$c>0$のとき
\begin{equation}\frac{a}{c}<\frac{b}{c}\end{equation}
となります。
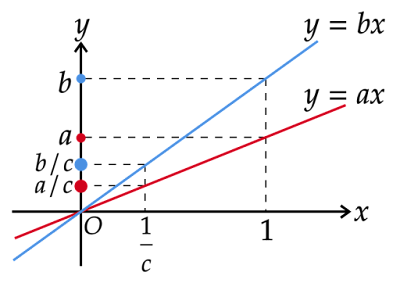
この操作を座標平面で見ると以下のようになります。
掛ける場合と同様、2つの直線$y=ax,y=bx$を考えます。
定数$c$で割ることは$c$の逆数$\dfrac{1}{c}$を掛けることに等しいので、この操作は$x$が$1$から$\dfrac{1}{c}$に変化することを意味します。
$x=\dfrac{1}{c}$における2つの直線上のそれぞれの点$\left(\dfrac{1}{c},\dfrac{a}{c}\right),\left(\dfrac{1}{c},\dfrac{b}{c}\right)$に着目すれば良いことがわかります。
正の定数$c$の逆数$\dfrac{1}{c}$もまた正の定数であるため、2点はx軸の正の部分$x>0$に存在しています。
直線の傾きと点の存在範囲より、点$\left(\dfrac{1}{c},\dfrac{b}{c}\right)$のほうが点$\left(\dfrac{1}{c},\dfrac{a}{c}\right)$よりも上に位置しています。
したがって、2点のy座標の大小関係より$(5)$が成り立つことがわかります。
$c$が負の定数のとき
$c$が負の定数、すなわち$c<0$のとき
\begin{equation}\frac{a}{c}>\frac{b}{c}\end{equation}
となります。
この操作を座標平面で見ると以下のようになります。
$x=\dfrac{1}{c}$における2つの直線$y=ax,y=bx$上のそれぞれの点$\left(\dfrac{1}{c},\dfrac{a}{c}\right),\left(\dfrac{1}{c},\dfrac{b}{c}\right)$について考えます。
負の定数$c$の逆数$\dfrac{1}{c}$もまた負の定数であるため、2点はx軸の負の部分$x<0$に存在しています。
直線の傾きと点の存在範囲より、点$\left(\dfrac{1}{c},\dfrac{a}{c}\right)$のほうが点$\left(\dfrac{1}{c},\dfrac{b}{c}\right)$よりも上に位置しています。
したがって、y座標に着目すると$(6)$が成り立つことがわかります。
なお、$0$で割ることはできないので、$c=0$の場合を考えることはできません。
また、両辺を定数$c$で割る操作を比例のグラフをもちいて表しましたが、反比例のグラフでも同様に表すことができます。
Share:
https://p-suugaku.blogspot.com/2023/09/futoushiki-kihonsousa.html数直線で見る不等式を解く基本的な4つの操作
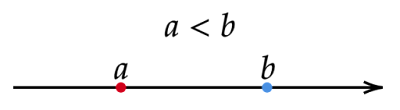
.png)
.png)
.png)
.png)
.png)



