円周角の定理の逆 なぜ成り立つ？

　円周角の定理とは、

1. 1つの弧に対する円周角の大きさは一定である。

2. 1つの弧に対する中心角の大きさは同じ弧に対する円周角の2倍である。

の2つのことを指します。

しかし、円周角の定理の逆とされるものは

1.の逆: 2点$\text{C, D}$が直線$\text{AB}$に関して同じ側にあるような4点$\text{A, B, C, D}$について、$∠\text{ACB}=∠\text{ADB}$が成り立つとき4点は同一円周上にある。

しかありません。それはなぜなのでしょうか？

1.の逆

　1.の逆が「2点$\text{C, D}$が直線$\text{AB}$に関して同じ側にあるような4点$\text{A, B, C, D}$について、$∠\text{ACB}=∠\text{ADB}$が成り立つとき4点は同一円周上にある。」となるのはなぜなのかについてまずは考えてみます。

円周角の定理の1.は

2点$\text{C, D}$が直線$\text{AB}$に関して同じ側にあるような4点$\text{A, B, C, D}$について、これら4点が同一円周上にあるならば$∠\text{ACB}=∠\text{ADB}$が成り立つ。

と書けます。
また、1.の逆の「～成り立つとき～」は「～成り立つならば～」に書き換えることができ、1.も1.の逆も命題の形をとっていることがわかります。

「2点$\text{C, D}$が直線$\text{AB}$に関して同じ側にあるような4点$\text{A, B, C, D}$について」という前提部分を除いて1.と1.の逆を比較すると「ならば」の前後が入れ替わっています。
「ならば」の前後を入れ替えた命題は逆の命題なので、1.と1.の逆は互いに逆の命題であることがわかります。

ちなみに、4点$\text{A, B, C, D}$に対しての「2点$\text{C, D}$が直線$\text{AB}$に関して同じ側にある」という条件は1.においては同じ弧に対する円周角をつくるための位置条件です。

1つの弧に対する円周角はその弧上に頂点が存在することない、すなわち円周角の頂点の存在範囲は必ず弧の両端を通る直線に関して弧を含まない側になります。
4点$\text{A, B, C, D}$だけでは$∠\text{ACB},∠\text{ADB}$が１つの弧に対する円周角にならない場合があるので、この位置条件が必要になります。
前提部分は逆の命題でも共通するので1.の逆にも同様に付きます。

　では、1.の逆が成り立つことを確かめます。

「4点$\text{A, B, C, D}$が同一円周上にある」は「3点$\text{A, B, C}$がある同一円周上に点$\text{D}$もある」と言い換えられます。
すると、1.の逆の命題が偽であると仮定するならば、その反例は「$∠\text{ACB}=∠\text{ADB}$が成り立つが点$\text{D}$が3点$\text{A, B, C}$がある同一円周上にない」ことを示すものとなります。
そこで「点$\text{D}$が3点$\text{A, B, C}$がある同一円周上になくても$∠\text{ACB}=∠\text{ADB}$が成り立つ」ことがないということを示します。
これが示せれば反例の存在する余地がないので1.の逆の命題が真であることがわかります。

点$\text{D}$が3点$\text{A, B, C}$を通る円の外部にある場合

　点$\text{D}$が3点$\text{A, B, C}$を通る円$\text{O}$の外部にある場合を考えます。

円$\text{O}$と線分$\text{BD}$の交点を$\text{P}$とすると円周角の定理より$∠\text{ACB}=∠\text{APB}$が成り立ちます。
また、仮定より$∠\text{ACB}=∠\text{ADB}$が成り立ちます。

すると$∠\text{ADB}=∠\text{APB}$となり、これら2角は同位角なので$\text{AD}//\text{AP}$が成り立ちます。
しかし、$\text{AD}$と$\text{AP}$は点$\text{A}$で交わるので$\text{AD}//\text{AP}$と矛盾します。

したがって仮定は誤りであり、少なくとも点$\text{D}$は円$\text{O}$の外部には存在しません。

点$\text{D}$が3点$\text{A, B, C}$を通る円の内部にある場合

　点$\text{D}$が3点$\text{A, B, C}$を通る円$\text{O}$の内部にある場合を考えます。

円$\text{O}$と半直線$\text{BD}$の交点を$\text{P}$とすると円周角の定理より$∠\text{ACB}=∠\text{APB}$が成り立ちます。
また、仮定より$∠\text{ACB}=∠\text{ADB}$が成り立ちます。

すると$∠\text{ADB}=∠\text{APB}$となり、同位角が等しいので$\text{AD}//\text{AP}$が成り立ちます。
しかし、$\text{AD}$と$\text{AP}$は点$\text{A}$で交わるので$\text{AD}//\text{AP}$と矛盾します。

したがって仮定は誤りであり、点$\text{D}$は円$\text{O}$の内部にも存在しません。

　以上より、直線$\text{AB}$に関して点$\text{C}$と同じ側にあって$∠\text{ACB}=∠\text{ADB}$を満たす点$\text{D}$があるのは3点$\text{A, B, C}$を通る円の外部でも内部でもなく、その円周上のみであることがわかります。

したがって、「点$\text{D}$が3点$\text{A, B, C}$がある同一円周上になくても$∠\text{ACB}=∠\text{ADB}$が成り立つ」という仮定は否定され、1.の逆の命題が真であることが確かめられました。

2.の逆

　まず、2.の逆はどのような命題になるでしょうか？

円周角の定理の2.は

4点$\text{A, B, C, D}$について、点$\text{D}$が3点$\text{A, B, C}$を通る円の中心であるならば$2∠\text{ACB}=∠\text{ADB}$が成り立つ。

と書けます。
すると、2.の逆は

4点$\text{A, B, C, D}$について、$2∠\text{ACB}=∠\text{ADB}$が成り立つならば点$\text{D}$は3点$\text{A, B, C}$を通る円の中心である。

となります。

ちなみに、1.と違い4点$\text{A, B, C, D}$に対して「2点$C, D$が直線$\text{AB}$に関して同じ側にある」がないのは、同じ弧に対する円周角と中心角にはこの条件が必ずしも当てはまるわけではないためです。

円周角が鋭角のとき、「2点$C, D$が直線$\text{AB}$に関して同じ側にある」は成り立ちますが、円周角が直角のときは点$\text{D}$は直線$\text{AB}$上（線分$\text{AB}$の中点）、
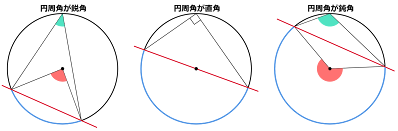
円周角が鈍角のときは点$\text{C}$と$\text{D}$は直線$\text{AB}$に関して互いに反対側に存在します。
2.の命題は前提がなくとも真となるので、1.のような位置条件を加える必要がありません。

　では、なぜ2.の逆の命題が偽なのかを考えます。

$∠\text{ACB}$が鋭角または鈍角の場合

　$2∠\text{ACB}=∠\text{ADB}$が成り立つように4点$\text{A, B, C, D}$をとります。ただし、$∠\text{ACB}$は鋭角または鈍角とします。
2.の逆が成り立つと仮定すれば点$\text{D}$は3点$\text{A, B, C}$を通る円$\text{O}$の中心となります。

ここで3点$\text{A, B, D}$を通る円を描き、この円周上の直線$\text{AB}$に関して点$\text{D}$と同じ側に点$\text{D}$とは異なる点$\text{Q}$をとります。
すると円周角の定理より$∠\text{ADB}=∠\text{AQB}$が成り立ちます。すなわち$2∠\text{ACB}=∠\text{AQB}$が成り立つため2.の逆より点$\text{Q}$が円$\text{O}$の中心となります。
しかし、これは円$\text{O}$の中心は点$\text{D}$であるということに矛盾します。

したがって仮定は誤り、すなわち$∠\text{ACB}$が鋭角または鈍角の場合、2.の逆は偽であることがわかります。

上図は$∠\text{ACB}$が鋭角の場合のものですが、鈍角の場合も同様です。

$∠\text{ACB}$が直角の場合

　$∠\text{ACB}$が直角で$2∠\text{ACB}=∠\text{ADB}$が成り立つように4点$\text{A, B, C, D}$をとります。このとき、$∠\text{ADB}=180°$となるので点$\text{D}$は線分$\text{AB}$上の点となります。
この場合でも$∠\text{ACB}$が鋭角または鈍角の場合同様、2.の逆が成り立つと仮定すれば点$\text{D}$が3点$\text{A, B, C}$を通る円$\text{O}$の中心となります。

ここで、線分$\text{AB}$上に点$\text{D}$とは異なる点$\text{Q}$をとれば$∠\text{AQB}=180°$となり、$2∠\text{ACB}=∠\text{AQB}$が成り立つため2.の逆より点$\text{Q}$が円$\text{O}$の中心となります。
しかし、これは円$\text{O}$の中心は点$\text{D}$であるということに矛盾します。

したがって、仮定は誤り、すなわち$∠\text{ACB}$が直角の場合でも2.の逆は偽であることがわかります。

　円周角の大きさは$180°$未満なので、以上より円周角$∠\text{ACB}$がいずれの大きさを持っていたとしても仮定は誤り、すなわち2.の逆が偽となることがわかります。

　以上より、円周角の定理の逆として常に成り立つのは1.の逆である「2点$C, D$が直線$\text{AB}$に関して同じ側にあるような4点$\text{A, B, C, D}$について、$∠\text{ACB}=∠\text{ADB}$が成り立つとき4点は同一円周上にある。」だけとなります。

関連：円周角の定理 なぜ成り立つのか？

関連：同一円周上に4点がある場合とは？