三角形の外心と垂心と重心の関係 オイラー線

三角形の外心、垂心、重心の間には以下のような関係があります。

「三角形の外心、垂心、重心は同一直線上に存在する。」

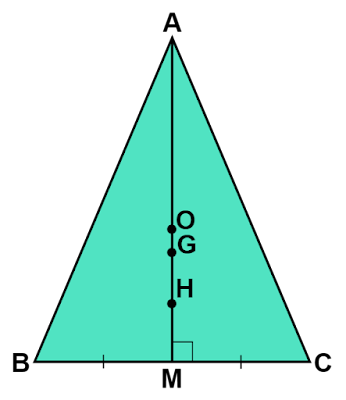
上図のように$△\text{ABC}$の外心$\text{O}$、垂心$\text{H}$、重心$\text{G}$の3点は必ず一直線上に並びます。

これが成り立つことを確かめてみます。

　このことを確かめるために三角形の外心と垂心の関係を利用します。

鋭角三角形の場合

　鋭角三角形$\text{ABC}$の外心を$\text{O}$、垂心を$\text{H}$、辺$\text{BC}$の中点を$\text{M}$、線分$\text{AM}$と$\text{OH}$の交点を$\text{P}$とします。

$△\text{AHP}$と$△\text{MOP}$に着目すると、
$\text{AH, OM}$はともに辺$\text{BC}$に対し垂直なので$\text{AH}//\text{OM}$です。
上記より錯角は等しいので$∠\text{HAP}=∠\text{OMP, }∠\text{AHP}=∠\text{MOP}$です。
2組の角がそれぞれ等しいので相似であることがわかります。
その相似比は、三角形の外心と垂心の関係より$\text{AH}:\text{MO}=2:1$。また、$\text{AP}:\text{MP}=2:1$でもあります。

ここで、線分$\text{AM}$は$△\text{ABC}$の中線の1本で、点$\text{P}$は中線$\text{AM}$を$2:1$に内分する点ということになります。

そして$△\text{ABC}$の重心もまた中線$\text{AM}$を$2:1$に内分するので点$\text{P}$は重心であることがわかります。

重心$\text{P}$は外心$\text{O}$と垂心$\text{H}$を結ぶ直線$\text{OH}$上に存在するため、鋭角三角形の外心、垂心、重心は同一直線上に存在することがわかります。

直角三角形の場合

　$∠\text{A}=90°$である直角三角形$\text{ABC}$の垂心は頂点$\text{A}$にあり、外心$\text{O}$は斜辺$\text{BC}$の中点にあります。

線分$\text{AO}$は直角三角形$\text{ABC}$の中線となるので、重心$\text{G}$は$\text{AO}$上に存在しています。

したがって、直角三角形の外心、垂心、重心は同一直線上に存在することがわかります。

鈍角三角形の場合

　$∠\text{A}$が鈍角である鈍角三角形$\text{ABC}$の垂心を$\text{H}$、辺$\text{BC}$の中点を$\text{M}$、線分$\text{AM}$と$\text{OH}$の交点を$\text{P}$とします。

$△\text{AHP}$と$△\text{MOP}$に着目すると、
$\text{AH, OM}$はともに辺$\text{BC}$に対し垂直なので$\text{AH}//\text{OM}$です。
上記より錯角は等しいので$∠\text{HAP}=∠\text{OMP, }∠\text{AHP}=∠\text{MOP}$です。
2組の角がそれぞれ等しいので相似であることがわかります。
その相似比は、三角形の外心と垂心の関係より$\text{AH}:\text{MO}=2:1$。また、$\text{AP}:\text{MP}=2:1$でもあります。

点$\text{P}$は中線$\text{AM}$を$2:1$に内分する点なので、点$\text{P}$は$△\text{ABC}$の重心であることがわかります。

重心$\text{P}$は外心$\text{O}$と垂心$\text{H}$を結ぶ直線$\text{OH}$上に存在するため、鋭角三角形の外心、垂心、重心は同一直線上に存在することがわかります。

二等辺三角形の場合

　上の3つの場合分けですべての三角形の場合を考えたように思えますが、実は例外があります。それは二等辺三角形の場合です。

　$\text{AB}=\text{AC}$である二等辺三角形$\text{ABC}$の外心$\text{O}$、垂心$\text{H}$、重心$\text{H}$はすべて底辺$\text{BC}$の垂直二等分線上に存在します。これは底辺の垂直二等分線が外心が存在している「辺の垂直二等分線」であり、垂心が存在している「頂点から対辺へおろした垂線」でもあり、重心が存在している「中線」でもあるためです。

したがって、二等辺三角形の外心、垂心、重心は同一直線上に存在することがわかります。

鋭角三角形または鈍角三角形で二等辺三角形である場合、中線と外心と垂心を結ぶ直線が重なってしまうため、三角形の相似を利用する方法が使えないので例外となります。

　また、二等辺三角形の中でも特殊である正三角形の外心、垂心、重心はすべて一点に集まっています。

したがって、他の三角形においては外心、垂心、重心の3点を通る直線はただ1つであるのに対し、正三角形においてはこれら3点を通る直線は無数に存在します。

　三角形の外心、垂心、重心の3点を通る直線のことをオイラー線といいます。これは1つの三角形に対し1本存在します。

しかし、外心、垂心、重心の3点を通る直線が無数に存在する正三角形のみオイラー線を定義できません。

関連：三角形の外心と垂心の関係

関連：三角形の外心が３辺の垂直二等分線の交点で求められるのはナゼ？

関連：三角形の垂心

関連：三角形の重心とその性質