円に内接・外接する正多角形の面積を求めるための式を作ってみようと思います。
円に内接する正多角形の面積

|
| 図1 円に内接する正多角形 |
半径$r$の円の中心を通る正$n$角形の対角線を引くと、合同な二等辺三角形が$n$個できます。
二等辺三角形の頂角の大きさは$\frac{360°}{n}$、等辺は外接円の半径でもあるのでその長さは$r$です。
この二等辺三角形の面積$s_{ni}$は
\begin{align*}s_{ni}&=\frac{1}{2}r\cdot
r\sin\frac{360°}{n}\\[0.5em]&=\frac{r^2}{2}\sin\frac{360°}{n}\end{align*}
二等辺三角形は$n$個あるので、円に内接する正$n$角形の面積$S_{ni}$は
\[S_{ni}=n\cdot s_{ni}\]
であるので、
\[\mathbf{S_{ni}=\frac{nr^2}{2}\sin\frac{360°}{n}}\qquad(n:3\text{以上の整数})\]
より求められます。
円に外接する正多角形の面積
|
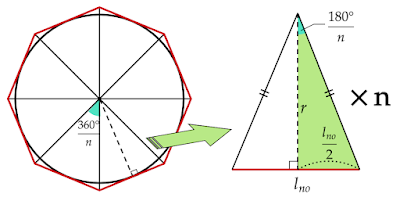
| 図2 円に外接する正多角形 |
半径$r$の円の中心を通る正$n$角形の対角線を引くと、合同な二等辺三角形が$n$個できます。
二等辺三角形の頂角の大きさは$\frac{360°}{n}$、高さは半径と等しいので$r$です。
高さを利用して二等辺三角形の面積を求めるには底辺の長さ$l_{no}$が必要になります。
そこで、図2の緑の直角三角形を利用します。
この直角三角形の鋭角の1つは二等辺三角形の頂角の半分の大きさであるため
\[\frac{360°}{n}\cdot\frac{1}{2}=\frac{180°}{n}\]
で、この角の対辺の長さは二等辺三角形の底辺の半分の長さなので$\dfrac{l_{no}}{2}$です。このことから
\begin{align*}\frac{l_{no}}{2}&=r\tan\frac{180°}{n}\\[0.5em]l_{no}&=2r\tan\frac{180°}{n}\end{align*}
ここで、半角の公式
\[\tan\frac{\theta}{2}=\frac{\sin\theta}{1+\cos\theta}\]
より
\begin{align*}l_{no}&=2r\tan\frac{180°}{n}\\[0.5em]&=2r\tan\frac{\frac{360°}{n}}{2}\\[0.5em]&=2r\frac{\sin\frac{360°}{n}}{1+\cos\frac{360°}{n}}\end{align*}
したがって、二等辺三角形の面積$s_{no}$は、
\begin{align*}s_{no}&=\frac{1}{2}r\cdot
l_{no}\\[0.5em]&=\frac{1}{2}r\cdot2r\frac{\sin\frac{360°}{n}}{1+\cos\frac{360°}{n}}\\[0.5em]&=\frac{r^2\sin\frac{360°}{n}}{1+\cos\frac{360°}{n}}\end{align*}
二等辺三角形は$n$個あるので、円に外接する正$n$角形の面積$S_{no}$は
\[S_{no}=n\cdot s_{no}\]
であるので、
\[\mathbf{S_{no}=\frac{nr^2\sin\frac{360°}{n}}{1+\cos\frac{360°}{n}}}\quad(n:3以上の整数)\]
となります。
(2024/3)半角の公式に誤りがありましたので修正しました。申し訳ございません。
Share:



