行列で掛け算ができるのは？

「上の行列の積のAに当てはまる掛け算が可能な行列を(a)～(e)の中からすべて選び、その積を答えよ。」

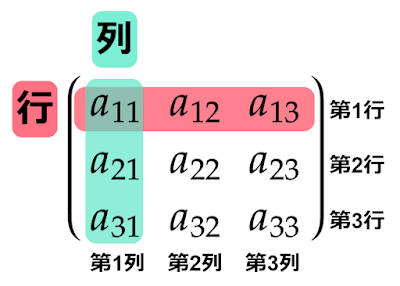
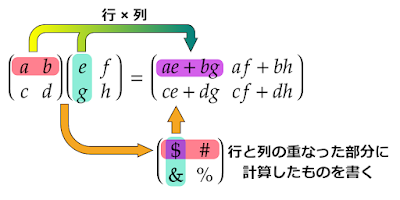
　まず行列について。

図1　行列

行列の数の並びには行と列があり、横の並びが行、縦の並びが列です。

　これを踏まえて行列の掛け算を考えます。

図2　行列の掛け算

行列の掛け算は、行×列で計算します。
図2のように2行2列の行列同士の掛け算で掛けられる行列の第1行と掛ける行列の第1列を計算する場合、

第1行第1列(a) × 第1行第1列(e) + 第1行第2列(b) × 第2行第1列(g)

という計算をします。この計算結果を積となる行列のどこに書くかについては、

第1行×第1列の計算であれば第1行第1列に、第1行×第2列の計算であれば第1行第2列というように、行列の計算に使った場所を組み合わせることでどこに書くべきかが決まります。

また、掛け算ができる行列は掛けられる行列の1行に含まれる数の個数と掛ける行列の1列に含まれる数の個数が同じでなければなりません。すなわち、行列の掛け算は行×列で行いますが、掛け算が可能であるかは列数と行数で判断します。

　以上のことから問題について考えると、掛ける行列の1列には3つの数が含まれている、すなわち3行であることから掛け算が可能な行列は3列の行列であることがわかります。

したがって、(a)、(b)、(c)の3つが掛け算可能な行列となります。

それぞれの場合の積は、

・(a)

\begin{align*}&(\begin{array}{r}1&1&1\end{array})\left(\begin{array}{r}4&6&1\\ 5&2&3\\ 1&7&0\end{array}\right)\\ =&(\begin{array}{r}1\cdot4+1\cdot5+1\cdot1&1\cdot6+1\cdot2+1\cdot7&1\cdot1+1\cdot3+1\cdot0\end{array})\\ =&(\begin{array}{r}10&15&4\end{array})\end{align*}

・(b)

\begin{align*}&\left(\begin{array}{r}0&3&1\\ 2&0&1\end{array}\right)\left(\begin{aligned}4\quad6\quad1\\ 5\quad2\quad3\\ 1\quad7\quad0\end{aligned}\right)\\ =&\left(\begin{array}{r}0\cdot4+3\cdot5+1\cdot1&0\cdot6+3\cdot2+1\cdot7&0\cdot1+3\cdot3+1\cdot0\\ 2\cdot4+0\cdot5+1\cdot1&2\cdot6+0\cdot2+1\cdot7&2\cdot1+0\cdot3+1\cdot0\end{array}\right)\\ =&\left(\begin{array}{r}16&13&9\\ 9&19&2\end{array}\right)\end{align*}

・(c)

\begin{align*}&\left(\begin{array}{r}1&2&3\\ 3&1&2\\ 2&3&1\end{array}\right)\left(\begin{array}{r}4&6&1\\ 5&2&3\\ 1&7&0\end{array}\right)\\ =&\left(\begin{array}{r}1\cdot4+2\cdot5+3\cdot1&1\cdot6+2\cdot2+3\cdot7&1\cdot1+2\cdot3+3\cdot0\\ 3\cdot4+1\cdot5+2\cdot1&3\cdot6+1\cdot2+2\cdot7&3\cdot1+1\cdot3+2\cdot0\\ 2\cdot4+3\cdot5+1\cdot1&2\cdot6+3\cdot2+1\cdot7&2\cdot1+3\cdot3+1\cdot0\end{array}\right)\\ =&\left(\begin{array}{r}17&31&7\\ 19&34&6\\ 24&25&11\end{array}\right)\end{align*}

となります。