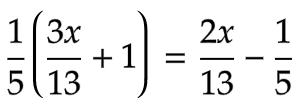分数がある1次方程式を解く

上の方程式を解け。

　このような問題はどのように解けばよいでしょうか？

　分数がある方程式は、両辺に同じ数を掛けて整数のみの方程式にしてから解きます。
分数の計算法則のうち、

\begin{align*}\frac{b}{a}+\frac{d}{c}&=\frac{ad+bc}{ac}\\[1em]\frac{b}{a}×\frac{d}{c}&=\frac{bd}{ac}\end{align*}

の分母に着目すると、足し算掛け算どちらの場合も分母の数の積となるので、両辺に$5×13=65$を掛ければ分母を払うことができます。

\[\frac{1}{5}\left(\frac{3x}{13}+1\right)×65=\left(\frac{2x}{13}-\frac{1}{5}\right)×65\]

　右辺、左辺それぞれ計算します。

右辺は分配法則を使います。

\begin{align*}(右辺)&=\frac{2x}{13}×65-\frac{1}{5}×65\\[0.5em]&=10x-13\tag{a}\end{align*}

左辺は先に$\dfrac{1}{5}\left(\dfrac{3x}{13}+1\right)$を計算してもよいのですが、少し計算を工夫することができます。
$65$を因数分解、その後交換法則と結合法則を利用します。

\begin{align*}(左辺)&=\frac{1}{5}\left(\frac{3x}{13}+1\right)×5×13\\[0.5em]&=\left(\frac{1}{5}×5\right)×\left\{\left(\frac{3x}{13}+1\right)×13\right\}\end{align*}

順番が変わっているのが交換法則、新たに括弧を書き加えたのが結合法則です。

\begin{align*}(左辺)&=1×\left(\frac{3x}{13}×13+1×13\right)\\[0.5em]&=3x+13\tag{b}\end{align*}

$5$と$\dfrac{1}{5}$は互いに逆数なので積は$1$になり、あとは分配法則を利用して計算します。

$\text{(a)}=\text{(b)}$なのでこれを解けば

\begin{align*}3x+13&=10x-13\\[0.5em]3x-10x&=-13-13\\[0.5em]-7x&=-26\\[0.5em]x&=\frac{-26}{-7}=\mathbf{\frac{26}{7}}\end{align*}

と$x$の値が求まります。