1次関数が互いに直交する条件は？

　1次関数が互いに直交するためにはどんな条件があるのかをいくつかの方法で調べてみました。

前提

図1　直交する直線と平行な直線

　直線$l:ax+by+c=0$と直線$s:px+qy+r=0$（ただし、c、rは0でない）が直交しているとき、原点を通り直線l、直線sそれぞれに平行な直線$m:ax+by=0$、$t:px+qy=0$を考えます。

平行線の性質より、直線lは直線tと直交することからlと平行な直線mもtと直交します。

lとm、sとtはそれぞれ切片が異なるだけで傾きは同じなので、直線（1次関数）が直交する条件は原点を通る直線についてのみ調べるだけで良いことがわかります。

また、原点を通る直線の傾きは原点以外であれば$\frac{y}{x}$で求めることができます。

1. 二等辺三角形の性質を利用

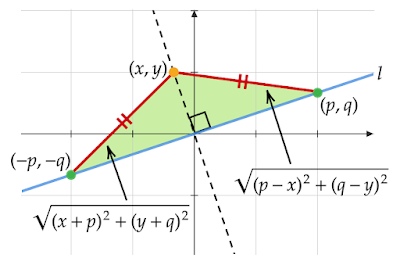図2　二等辺三角形の性質を利用

　原点を通る直線l上に原点以外の点(p, q)と原点に関して対称な点(-p,-q)の2点をおきます。
この2点と等距離にある点(x, y)をおくとこれら3点によって二等辺三角形ができ、(x, y)の軌跡は二等辺三角形の中線であるため直線lに対し垂直で原点を通る直線となります。

(p, q)と(x, y)との距離は

\[\sqrt{(p-x)^2+(q-y)^2}\]

(-p, -q)と(x, y)との距離は

\[\sqrt{(x+p)^2+(y+q)^2}\]

で、これらは等しいので、

\begin{align*}\sqrt{(p-x)^2+(q-y)^2}&=\sqrt{(x+p)^2+(y+q)^2}\\ (p-x)^2+(q-y)^2&=(x+p)^2+(y+q)^2\\ (p^2-2px+x^2)+(q^2-2qy+y^2)&=(x^2+2px+p^2)+(y^2+2qy+q^2)\\ px+qy&=0\end{align*}

となり、これを満たすx、yは

\[x=-kq,y=kp\ または\ x=kq,y=-kp\quad(k:任意の実数)\]

となります。すなわち(-kq, kp)または(kq, -kp)となる点ということです。

　したがって、直線lの傾きは$\frac{q}{p}$であるのに対しlに直交する直線の傾きは

\begin{align*}x=-kq,&y=kpのとき\\ &\frac{kp}{-kq}=-\frac{p}{q}\\ \\ x=kq,&y=-kpのとき\\ &\frac{-kp}{kq}=-\frac{p}{q}\end{align*}

となるので、互いに直交する直線の傾きの積は

\[\Large{\frac{p}{q}×\left(-\frac{q}{p}\right)=-1}\]

となることがわかります。

2. 半径の等しい2円の交点を利用

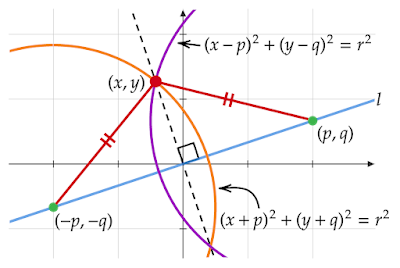図3　半径の等しい2円の交点

　原点を通る直線l上に原点以外の点(p, q)と原点に関して対称な点(-p, -q)をおきます。
この2点を中心とする半径の等しい円$(x-p)^2+(y-q)^2=r^2と(x+p)^2+(y+q)^2=r^2\quad(r\geqq \sqrt{p^2+q^2})$を考えます。

1. と同様に円の中心と2円の交点によって二等辺三角形ができ、円の半径を変化させることで直線lに直交する直線の軌跡を求めることができます。

2円の交点を求める方程式は

\begin{align*}(x-p)^2+(y-q)^2&=(x+p)^2+(y+q)^2\\ (x^2-2px+p^2)+(y^2-2qy+q^2)&=(x^2+2px+p^2)+(y^2+2qy+q^2)\\ px+qy&=0\end{align*}

となり、これを満たすx、yは

\[x=-kq,y=kp\ または\ x=kq,y=-kp\quad(k:任意の実数)\]

となるため、2円の交点の座標は$k\neq0$のとき(-kq, kp)、(kq, -kp)、$k=0$のとき(0, 0)と求まります。

原点を通ること、xとyの値がともにk倍され比例の関係にあることから2円の交点の軌跡は確かに原点を通る直線であることがわかります。

　以上より直線lに直交する直線の傾きは

\begin{align*}x=-kq,&y=kpのとき\\ &\frac{kp}{-kq}=-\frac{p}{q}\\ \\ x=kq,&y=-kpのとき\\ &\frac{-kp}{kq}=-\frac{p}{q}\end{align*}

となるため、互いに直交する直線の傾きの積は

\[\Large{\frac{q}{p}×\left(-\frac{p}{q}\right)=-1}\]

となることがわかります。

3. 三角関数を利用

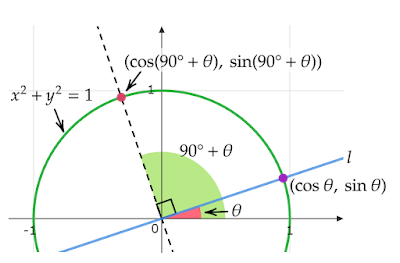図4　三角関数を利用

　原点を通る直線lと原点を中心とする半径1の円O$x^2+y^2=1$を描きます。
直線lとx軸のなす角をθとすると直線lと円Oの交点の1つは&(\cos\theta,\sin\theta)&となるため、直線lと直交する直線と円Oの交点の1つは$(\cos(90^{\circ}+\theta),\sin(90^{\circ}+\theta))$と表せます。

三角関数の性質より

\begin{align*}\cos(90^{\circ}+\theta)&=-\sin\theta\\ \\ \sin(90^{\circ}+\theta))&=\cos\theta\end{align*}

となるので、

\[(\cos(90^{\circ}+\theta),\sin(90^{\circ}+\theta))=(-\sin\theta,\cos\theta)\]

です。

　したがって、直線lの傾きは

\[\frac{\sin\theta}{\cos\theta}=\tan\theta\]

直線lに直交する直線の傾きは

\[\frac{\sin(90^{\circ}+\theta)}{\cos(90^{\circ}+\theta)}=\frac{\cos\theta}{-\sin\theta}=-\frac{1}{\tan\theta}\]

となるので、この2直線の傾きの積は

\[\Large{\tan\theta×\left(-\frac{1}{\tan\theta}\right)=-1}\]

となることがわかります。

4. ベクトルを利用

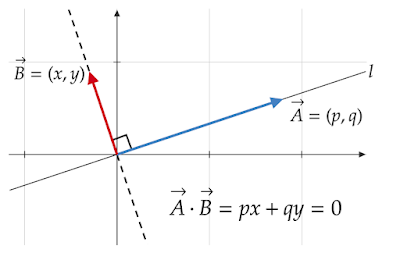図5　ベクトルを利用

　原点を通る直線l上に点(p, q)をとり、これを成分とする$\vec{A}=(p,q)$と、このベクトルに垂直な$\vec{B}=(x,y)$を考えます。

するとこの2つのベクトルの内積は

\[\vec{A}\cdot\vec{B}=px+qy=0\]

となり、これを満たすx, yは

\[x=-kq,y=kp\ または\ x=kq,y=-kp\quad(k:任意の実数)\]

となります。

したがって、$\vec{B}=(-kq,kp)$または$\vec{B}=(kq,-kp)$となりますが、$(-kq,kp)=-(kq,-kp)$なので、互いに向きが逆であるだけで同一直線上にあります。

ベクトルの成分は始点を原点としたときの終点の座標なので、$\vec{B}$の軌跡は原点を通る直線lに直交する直線であることがわかります。

　以上より直線lに直交する直線の傾きは

\begin{align*}x=-kq,&y=kpのとき\\ &\frac{kp}{-kq}=-\frac{p}{q}\\ \\ x=kq,&y=-kpのとき\\ &\frac{-kp}{kq}=-\frac{p}{q}\end{align*}

となるため、互いに直交する直線の傾きの積は

\[\Large{\frac{q}{p}×\left(-\frac{p}{q}\right)=-1}\]

となることがわかります。

　以上のように様々な方法で調べてみると2直線（1次関数）が互いに直交するための条件とは、2直線の傾きの積が$-1$となることがわかります。

直線の傾きにばかり言及して直線の方程式に触れていませんが、原点と(p, q)を通る直線l（3. の場合は$\cos\theta=p,\sin\theta=q$として）は

\begin{align*}\frac{q}{p}x-y&=0\\ \\ qx-py&=0\end{align*}

直線lに直交する直線は(-q, p)、(q, -p)を通るので

\begin{align*}\frac{-p-p}{q-(-q)}(x-q)-y-p&=0\\ \\ px+qy&=0\end{align*}

で表されます。

また、前提で述べたとおり原点を通る直線の直交するための条件は、平行線の性質によりあらゆる直線に対し適用できるので、任意の実数r、sをもちいて$qx-py+r=0$と$px+qy+s=0$もまた直交することがわかります。