長方形の面積と対角線の長さから1辺の長さを求める

「長方形の面積が$60$、対角線の長さが$13$であるとき、この長方形の長辺の長さを求めよ。」

　問題の長方形を長方形$\text{ABCD}$とし、辺$\text{AB, CD}$の長さを$a$、辺$\text{BC, DA}$の長さを$b$とおきます。
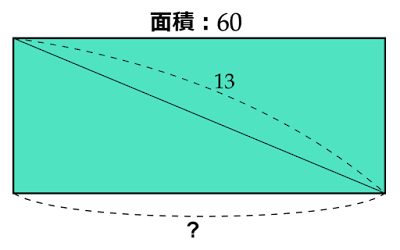
すると、長方形$\text{ABCD}$の面積は$60$なので

$$\begin{equation}ab=60\end{equation}$$

と式を立てることができます。

　次に、対角線$\text{AC}$を引くと問題の条件よりこの長さが$13$となります。
また、このときできる$△\text{ABC}$は$∠\text{ABC}$が直角の直角三角形なので、三平方の定理より

$$\begin{align*}\text{AB}^2+\text{BC}^2&=\text{AC}^2\\[0.5em]a^2+b^2&=13^2=169\tag2\end{align*}$$

が成り立ちます。

関連：三平方の定理（ピタゴラスの定理）

　$(1), (2)$を連立してこれらを満たす$a, b$を求めます。

$(a+b)^2$について考えると

$$\begin{align*}(a+b)^2&=a^2+2ab+b^2\\[0.5em]&=(a^2+b^2)+2\cdot ab\\[0.5em]&=169+2\cdot60&(\because (1), (2))\\[0.5em]&=289\end{align*}$$

となります。

両辺の平方根をとると$289=17^2$であること、$a>0, b>0$より$a+b>0$であることより

$$a+b=17\tag3$$

であることがわかります。

$(3)$を変形すると$b=17-a$となるので、これを$(1)$に代入すると

$$\begin{align*}a(17-a)&=60\\[0.5em]17a-a^2&=60\\[0.5em]a^2-17a+60=0\\[0.5em]a^2-(5+12)a+5\cdot12&=0\\[0.5em](a-5)(a-12)&=0\\[0.5em]a=5, 12\end{align*}$$

と2次方程式より$a$の値が求まります。

もちろん、解の公式をもちいて

$$\begin{align*}a&=\frac{-(-17)\pm\sqrt{(-17)^2-4\cdot60}}{2}\\[0.5em]&=\frac{17\pm\sqrt{49}}{2}\\[0.5em]&=\frac{17\pm7}{2}\\[0.5em]&=5, 12\end{align*}$$

と求めることもできます。

関連：2次方程式の解の公式と判別式

それぞれの場合における$b$の値を求め、どちらが長辺となるのかを調べます。

$a=5$のとき

　$b=17-a$より$b=12$なので、長辺の長さは$12$であることがわかります。

$a=12$のとき

　$b=17-a$より$b=5$なので、長辺の長さは$12$であることがわかります。

以上より、どちらも場合でも長方形の長辺の長さは$12$であることがわかります。