極座標とは

　極座標とは、基準となる固定された半直線と向きを定め、半直線の端点からの距離と基準の向きへの回転量によって点の位置を表す方法です。

基準となる固定された半直線を始線といい、始線の端点を原点または極といいます。始線が回転の開始位置となります。また、原点とある点を結ぶ線分を動径といい、その長さが原点からの距離を表します。
平面においては原点を中心として基準となる向きを1つ定めることになり、これは通常反時計回りと定められます。始線の開始位置と基準となる回転方向が定められているので、回転量を表すのに一般角をもちいます。この角度を偏角といいます。

関連：一般角とは？

原点からの距離を動径座標、始線からの回転量を偏角座標といいますが、動径、偏角だけでも同じ意味でもちいられることがあります。

点$P$の動径座標が$r$、偏角座標が$θ$であるとき、点$P$の位置を$(r,θ)$という数の組で表します。直交座標と同様、これも点$P$の座標といいます。直交座標も極座標も同じ形式で座標を表すので、あらかじめどちらの方法をもちいているかを書いておく必要があります。

例えば

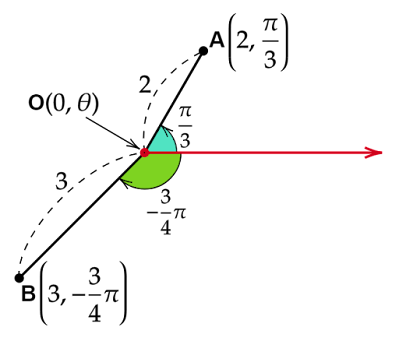
1. 点$A$の座標が$\left(2,\dfrac{\pi}{3}\right)$ならば、点$A$は原点から$2$の距離、始線から原点を中心に反時計回りに$\dfrac{\pi}{3}[\text{rad}]$だけ回転した位置にあります。
2. 点$B$の座標が$\left(3,-\dfrac{3}{4}\pi\right)$ならば、点$B$は原点から$3$の距離、始線から原点を中心に反時計回りに$-\dfrac{3}{4}\pi[\text{rad}]$（＝時計回りに$\dfrac{3}{4}\pi[\text{rad}]$）だけ回転した位置にあります。

異なる座標が同じ位置を示す

　この方法は異なる座標が同じ点の位置を表すことがあります。

原点の極座標について考えると

原点から$0$の距離にあるといえるので動径座標は$0$です。

このとき、原点が原点を中心としてどれだけ回転しても、逆に回転しなくても位置が変わりません。すなわち、偏角座標は原点の位置を表すのに影響しない要素となります。

したがって、原点の座標は

\[\large(0,θ)\quad(θ:\text{任意の実数})\]

と表せるため、原点を表す座標は無数にあります。

また、偏角座標が$θ$のときの動径と$θ+2n\pi$（ただし、$n:$整数）のときの動径は重なるため$(r,θ)$で表される点と$(r,θ+2n\pi)$で表される点は同じ位置にあります。
したがって、

\begin{equation}\large(r,\theta)=(r,\theta+2n\pi)\quad(n:\text{整数})\end{equation}

が成り立つため、やはり同じ点を表す座標は無数にあります。

上で例示した$2.$の点$B\left(3,-\dfrac{3}{4}\pi\right)$の場合、同じ位置を表す座標の1つとして$\left(3,-\dfrac{3}{4}\pi+2\pi\right)=\left(3,\dfrac{9}{4}\pi\right)$が挙げられます。

動径座標の拡張

　動径座標$r$は原点からの距離であるため通常非負実数となりますが、負の値をとれるように拡張することもできます。

$r>0$のとき、点$(-r,θ)$を点$(r,θ)$と原点に関して対称な位置にある点と定めます。

すると、$(-r,θ)$の点は$(r,θ)$の点を原点を中心に$\pi[\text{rad}]$だけ反時計回りに回転させた位置にあるといえるので

\begin{equation}\large(-r,\theta)=(r,\theta+\pi)\end{equation}

が成り立ちます。

これは$r<0$のときにも成り立ちます。

$r=-r'$（ただし$r'>0$）とおくと点$(r,θ)$は点$(r',θ)$と原点に関して対称な位置にあるので、点$(r',θ)$を原点を中心に$\pi[\text{rad}]$だけ反時計回りに回転させた位置にあるといえますが、点$(r',θ)$を原点を中心に$-\pi[\text{rad}]$だけ反時計回りに回転させた位置にあるともいえます。

したがって、

\begin{align*}(r,\theta)&=(-r',\theta)\\[0.5em]&=(r',\theta-\pi)\\[0.5em]&=(-r,\theta-\pi)\end{align*}

また、$θ-\pi=\varphi$とおけば$θ=\varphi+\pi$なので

\[(r,\varphi+\pi)=(-r,\varphi)\]

となり、$(2)$と同様の式を得ます。

さらに$(2)$に$(1)$の性質も加えれば

\begin{equation}\begin{aligned}(-r,\theta)&=(r,\theta+\pi+2n\pi)\\[0.5em]&=(r,\theta+2(n+1)\pi)&(n:\text{整数})\end{aligned}\end{equation}

と書くことができます。

このように動径座標を拡張すると偏角座標だけでなく、動径座標が異なる座標が同じ点の位置を表すようになります。

　直交座標ではすべての実数の組によってすべての点の位置を表しましたが、極座標はすべての実数の組をもちいずともすべての点の位置を表すことができます。

極座標で平面上のすべての点の位置を表すためには$r$と$θ$の範囲を例えば$r\geqq0$かつ$0\leqq\theta<2\pi$と定めればよいですが、直交座標と異なり平面上のすべての点と座標が1対1対応になることはなく、原点のみただ1つの座標によって表すことができません。

関連：直交座標と極座標