直交座標と極座標はどちらも位置を表す方法ですが、これらはどのような違いがあるでしょうか?
直交座標
直交座標とは、基準となる定点と互いに直交する向きを定め、定点からある点へ到達するために必要なそれぞれの向きへの移動量によってあらゆる点の位置を表す方法です。
基準となる固定された点(定点)を原点といいます。これが移動の始点となります。
また、平面においては2つの互いに直交する向きを基準の向きとして定めます。向きと原点からの移動量を合わせて表すために数直線をもちい、これら数直線を座標軸と呼びます。
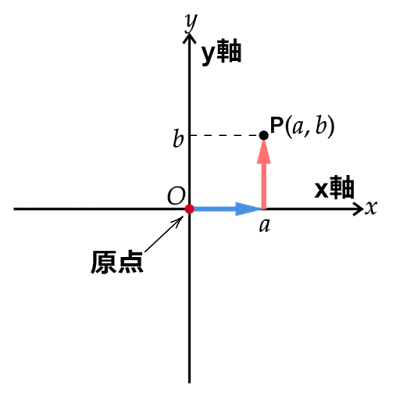
通常、横方向の座標軸をx軸、縦方向の座標軸をy軸とし、またそれぞれの方向への移動量をx座標、y座標と呼びます。
また、平面においては2つの互いに直交する向きを基準の向きとして定めます。向きと原点からの移動量を合わせて表すために数直線をもちい、これら数直線を座標軸と呼びます。
通常、横方向の座標軸をx軸、縦方向の座標軸をy軸とし、またそれぞれの方向への移動量をx座標、y座標と呼びます。
点$\text{P}$のx座標が$a$、y座標が$b$であるとき、点$\text{P}$の位置を$(a,b)$という数の組で表します。この数の組を点$\text{P}$の座標といいます。
例えば
- 点$\text{A}$の座標が$(3,2)$ならば、点$\text{A}$はx軸方向に$3$、y軸方向に$2$だけ移動した位置にあります。
- 点$\text{B}$の座標が$(-4,-3)$ならば、点$\text{B}$はx軸方向に$-4$、y軸方向に$-3$だけ移動した位置にあります。
- 原点$\text{O}$は原点から移動しない、すなわちx軸方向に$0$、y軸方向に$0$だけ移動した位置にあるといえるので原点$\text{O}$の座標は$(0,0)$と書けます。
極座標
極座標とは、基準となる固定された半直線と向きを定め、半直線の端点からの距離と基準の向きへの回転量によって点の位置を表す方法です。
基準となる固定された半直線を始線といい、始線の端点を原点または極といいます。始線が回転の開始位置となります。また、原点とある点を結ぶ線分を動径といい、その長さが原点からの距離を表します。
平面においては原点を中心として基準となる向きを1つ定めることになり、これは通常反時計回りと定められます。始線の開始位置と基準となる回転方向が定められているので、回転量を表すのに一般角をもちいます。この角度を偏角といいます。
平面においては原点を中心として基準となる向きを1つ定めることになり、これは通常反時計回りと定められます。始線の開始位置と基準となる回転方向が定められているので、回転量を表すのに一般角をもちいます。この角度を偏角といいます。
原点からの距離を動径座標、始線からの回転量を偏角座標といいますが、動径、偏角だけでも同じ意味でもちいられることがあります。
点$\text{P}$の動径座標が$r$、偏角座標が$θ$であるとき、点$\text{P}$の位置を$(r,θ)$という数の組で表します。直交座標と同様、これも点$\text{P}$の座標といいます。直交座標も極座標も同じ形式で座標を表すので、あらかじめどちらの方法をもちいているかを書いておく必要があります。
例えば
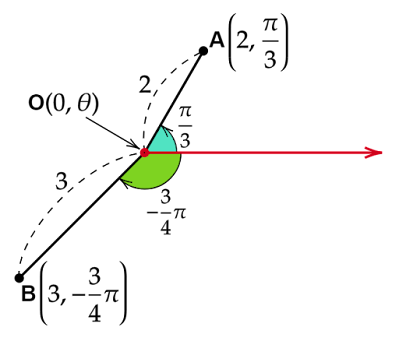
- 点$\text{A}$の座標が$\left(2,\dfrac{\pi}{3}\right)$ならば、点$\text{A}$は原点から$2$の距離、始線から原点を中心に反時計回りに$\dfrac{\pi}{3}[\text{rad}]$だけ回転した位置にあります。
- 点$\text{B}$の座標が$\left(3,-\dfrac{3}{4}\pi\right)$ならば、点$\text{B}$は原点から$3$の距離、始線から原点を中心に反時計回りに$-\dfrac{3}{4}\pi[\text{rad}]$(=時計回りに$\dfrac{3}{4}\pi[\text{rad}]$)だけ回転した位置にあります。
原点は極座標でも$(0,0)$かというと少し違います。
原点は原点から$0$の距離にあるといえるので動径座標は$0$です。
このとき、原点が原点を中心としてどれだけ回転しても、逆に回転しなくても位置が変わりません。すなわち、偏角座標は原点の位置を表すのに影響しない要素となります。
したがって、原点の座標は$(0,θ)$($θ:$任意の実数)と表されます。
このように直交座標と異なり原点を表す座標が複数存在しますが、実は原点以外の点についても同様に同じ点に複数の座標が存在します。
例えば、反時計回りに$2\pi[\text{rad}]$だけ回転すると元の位置に戻ってくるので$\left(2,\dfrac{7}{6}\pi\right)$と$\left(2,\dfrac{7}{6}\pi+2\pi\right)=\left(2,\dfrac{19}{6}\pi\right)$は同じ点の位置を表します。
Share:
.png)
.png)
.png)
.png)
.png)



