三角形と台形の中点連結定理

　中点連結定理とは、上図のように$△\text{ABC}$の2辺$\text{AB, AC}$の中点をそれぞれ$\text{M, N}$とすると

$$\large \text{BC}//\text{MN, BC}=2\text{MN}$$

が成り立つという定理です。

なぜこれが成り立つのでしょうか？確かめてみます。

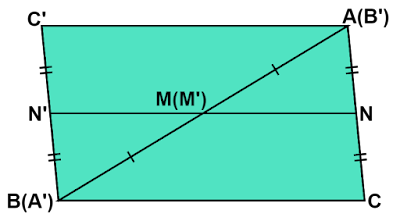
　$△\text{ABC}$と合同な$△\text{A'B'C'}$をつくり、辺$\text{A'B'}$の中点を$\text{M'}$、辺$\text{A'C'}$の中点を$\text{N'}$とします。
$△\text{A'B'C'}$を$180°$回転させ、辺$\text{AB}$と辺$\text{A'B'}$を重ねて四角形$\text{AC}’\text{BC}$をつくります。

このとき$\text{AM}=\text{BM}=\text{A'M'}=\text{B'M'}$なので点$\text{M}$と$\text{M'}$は重なり、3点$\text{M, N, N'}$は同一直線上にあります。$\text{MN}=\text{M'N'}$より

$$\begin{equation}\text{NN'}=2\text{MN}\end{equation}$$

が成り立ちます。

また、このように合同な三角形2つを組み合わせてできる四角形は平行四辺形なので、四角形$\text{AC'BC}$は平行四辺形です。このことから

$$\begin{equation}\text{AC}//\text{BC'}\end{equation}$$

であることがわかります。

ここで四角形$\text{BCNN'}$に着目すると、$(2)$と$\text{CN}=\text{BN'}$より1組の対辺が平行、かつ長さが等しいことから平行四辺形であることがわかります。このことから

$$\begin{equation}\text{BC}//\text{NN', BC}=\text{NN'}\end{equation}$$

です。

したがって、$(1), (3)$より$\text{BC}//\text{MN, BC}=2\text{MN}$であることがわかり、中点連結定理が成り立つことがわかります。

台形の中点連結定理

　台形にも中点連結定理があります。

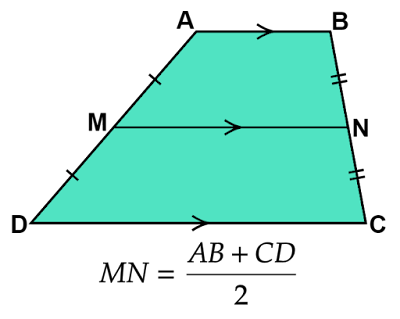
上図のように$\text{AB}//\text{CD}$である台形$\text{ABCD}$の$\text{AD, BC}$の中点をそれぞれ$\text{M, N}$とすると

$$\text{AB}//\text{MN}//\text{CD, MN}=\frac{\text{AB}+\text{CD}}{2}$$

が成り立ちます。

こちらも成り立つことを確かめてみます。

　台形$\text{ABCD}$に半直線$\text{AN}$を引き、$\text{CD}$の延長との交点を$\text{E}$とします。

$△\text{ABN}$と$△\text{ECN}$に着目します。
$\text{N}$は$\text{BC}$の中点なので$\text{BN}=\text{CN}$です。
$\text{AB}//\text{CD}$より錯角は等しいので$∠\text{ABN}=∠\text{ECN}$です。
対頂角なので$∠\text{ANB}=∠\text{ENC}$です。
1組の辺とその両端の角がそれぞれ等しいので$△\text{ABN}$と$△\text{ECN}$は合同であり、$\text{AN}=\text{EN, AB}=\text{CE}$であることがわかります。

　次に$△\text{ABE}$に着目すると$\text{M, N}$はそれぞれ$\text{AD, AE}$の中点となるので、三角形の中点連結定理より$\text{DE}//\text{MN, MN}=\dfrac{1}{2}\text{DE}$が成り立つことがわかります。

$\text{AB}//\text{CD}$かつ$\text{DE}//\text{MN}$より$\text{AB}//\text{MN}//\text{CD}$となります。
$\text{AB}=\text{CE}$より$\text{DE}=\text{CD}+\text{CE}=\text{AB}+\text{CD}$なので、

$$\begin{align*}\text{MN}&=\frac{1}{2}\text{DE}\\[0.5em]&=\frac{1}{2}(\text{AB}+\text{CD})\\[0.5em]&=\frac{\text{AB}+\text{CD}}{2}\end{align*}$$

となります。

したがって、台形の中点連結定理が成り立つことがわかります。

関連：中点連結定理の逆は成り立つ？