垂直二等分線上の点以外に等距離の点は存在する？

　ある線分の垂直二等分線上のすべての点はその線分の両端までの距離が等しいという性質があります。

垂直二等分線上の点以外に線分の両端までの距離が等しい点が存在しないことを確かめてみます。

まずは、ある線分の垂直二等分線上のすべての点はその線分の両端までの距離が等しいことを確かめます。

　線分$\text{AB}$の垂直二等分線$l$を引き、線分$\text{AB}$との交点を$\text{M}$とします。

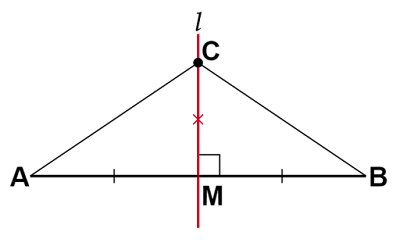
点$\text{M}$以外の直線$l$上の任意の点$\text{C}$をとり、2つの三角形$△\text{ACM}$と$△\text{BCM}$に着目すると、

• 点$\text{M}$は線分$\text{AB}$の中点でもあるので$\text{AM}=\text{BM}\ \cdots(\text{i})$
• 直線$l$は線分$\text{AB}$に対し垂直なので$∠\text{AMC}=∠\text{BMC}=90°\ \cdots(\text{ii})$
• 共通の辺なので$\text{CM}=\text{CM}\ \cdots(\text{iii})$

$\text{(i), (ii), (iii)}$より2組の辺の長さとその間の角がそれぞれ等しいので、$△\text{ACM}$と$△\text{BCM}$は合同であることがわかります。
このことから、$\text{AC}=\text{BC}\ \cdots(\text{iv})$です。

$\text{(i), (iv)}$より、ある線分の垂直二等分線上のすべての点はその線分の両端までの距離が等しいことがわかります。

　次に、垂直二等分線上の点以外に線分の両端までの距離が等しい点が存在しないことを背理法を利用して確かめてみます。

　垂直二等分線$l$上の点以外に線分の両端までの距離が等しい点$\text{P}$が存在すると仮定します。

点$\text{P}$から線分$\text{AB}$またはその延長へ垂線をおろし、その足を$\text{N}$とします。
このとき、線分$\text{AB}$の中点$\text{M}$は直線$l$上に存在するため、点$\text{M}$と$\text{N}$は一致しません。すなわち$\text{AN}\neq \text{BN}\ \cdots(*)$となります。

　$△\text{ANP}$と$△\text{BNP}$に着目すると

• 仮定より$\text{AP}=\text{BP}\ \cdots(\text{v})$
• 線分$\text{PN}$は線分$\text{AB}$に対し垂直なので$∠\text{ANP}=∠\text{BNP}=90°\ \cdots(\text{vi})$
• 共通な辺より$\text{PN}=\text{PN}\ \cdots(\text{vii})$

$\text{(v), (vi), (vii)}$より2組の辺の長さとその間の角がそれぞれ等しいので、$△\text{ANP}$と$△\text{BNP}$は合同であるとわかります。
すると、このことから$\text{AN}=\text{BN}$が成り立ち、$(*)$と矛盾するため仮定は誤りであることがわかります。

したがって、垂直二等分線上の点以外に線分の両端までの距離が等しい点が存在しないことがわかります。